Series 5, Year 19
Upload deadline: -, CET
1. what a stability of a ship
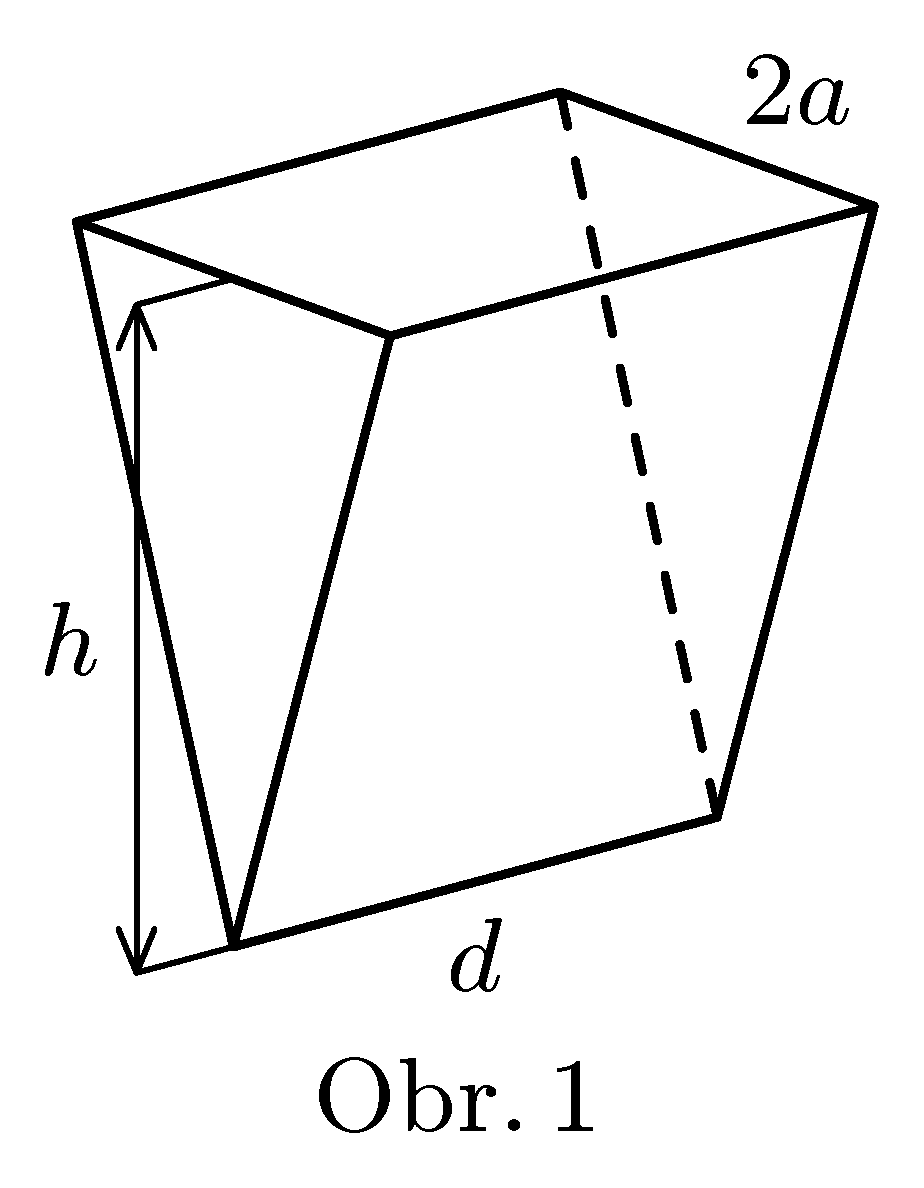
Scientists in NASA discovered special sediments of vegetable origin at Europa (Jupiter's moon). They are suitable for making very strong planks of oblong shape or triangular shape and are ideal for building a ship of height $h$, length $d$ and width 2$a$ (see figure 1) Help: captain to decide for which range of densities of ocean it is safe to sail such boat.
Assume that planks have constant thickness and density $ρ_{m}$ and that the ship is hollow and has a deck. (discuss the case when the ship is not hollow and has constant density $ρ_{m}.)$ It is not necessary to show just one final equation, more important is practical recipe (including all required equations) how to make such calculations. Try to make it simple to understand and explain all approximations made.
Vymyslel Pavel Brom při vzpomínce na historku o jedné nešťastně navržené lodi.
2. PET at a window
A PET bottle was left at a window in a well heated room. The temperature outside is well bellow zero Celsius. Someone opened the window and forget to close it and temperature in the room is now also well under zero. What is relative change of volume of bottle at a window?
Úlohu vymyslel Jano Lalinský.
3. efficiency of power station
Calculate the efficiency of a machine working between two thermal baths of temperatures $T_{1}$ and $T_{2}$, $T_{1}>T_{2}$ which is making biggest possible power. To final equation substitute data from some known power station.
Do not forgot, that Carnot's engine has zero output, because at isothermal process the difference of temperatures between the engine and the bath is infinitesimally small which causes infinitesimally small heat flux causing infinitesimally small output power of the engine.
Úloha z knížky Herbert Callen.
4. natural nuclear reactor
The typical composition of natural uranium is 0.72 % of isotope ^{235}U of halftime of 704 million years and the rest is isotope ^{238}U with half life of 4 468 million years.
While mining uranium in 1970's in Okla in equatorial Gabon, the uranium ore with relative content of isotope ^{235}U 0.44 % . This discrepancy can be explained by assuming existence of 'natural nuclear reactor' at the uranium deposits million years ago.
Calculate, how long the nuclear reaction was going on if the decay of ^{235}U was started by slow neutrons. The collision of slow neutron with the nucleus happens every 352 thousand years.
Úloha ze zápočtové písemky z jaderné fyziky.
P. about a lost well
An old couple is occupying theirs old house with their own well for drinking water. One day the water from the well stopped running, probably because of some problem in the well itself. Unfortunately, no one knows where the well is located.
From the pump, which is inside the house, 1.5 inch pipe goes approximately one meter underground and turns at right angle and continues in direction 'outside of the house' in horizontal direction. The well is filled with some material, and it is not clear, if is in the garden or under the house.
Suggest several possibilities of finding the well which are easy to realise.
V reálném životě na problém narazil Marek Scholz.
E. grandma's pancakes
Heat up a pan on the heat source to temperature ideal for pancake preparation (approx 200° C). If you drop a drop of water it will not evaporate immediately and will be running on the pan for up to one minute. Measure the time of life of the drop versus the size of the drop and try to explain.
Úlohu navrhl Jan Lalinský.
S. fermions and bosons
- Find a density of states $g(E)$ for free electrons and using this equation find relation between number of electrons and Fermi energy at zero temperature. Find out, what must be the Fermi energy dependence on temperature (for low temperatures) for constant number of electrons. Estimate number of excited electrons at room temperature
Hint: Take inspiration from last parts of our series and the problems accompanying them.
- Calculate dependence of μ versus temperature at low temperatures and constant number of particles in the system o identical bosons. Find the temperature dependence of number of excited bosons at low temperatures.
Zadal autor seriálu Matouš Ringel.