Seriál 12. ročníku
Celý seriál je také možné nalézt v ročence.
Úlohy
1. Série 12. Ročníku - S. dalekohledy a čočky
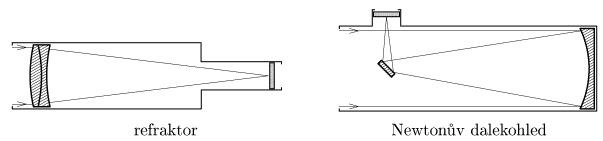

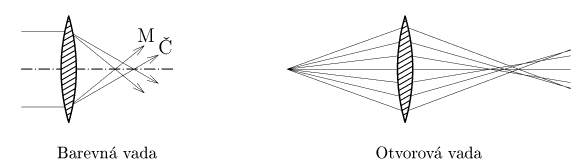
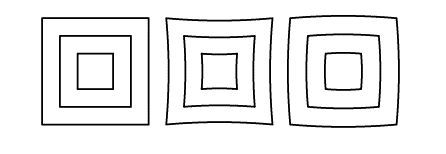
- Kolikrát slabší hvězdy bude schopen zaznamenat dalekohled VLT, který se staví na La Silla, Chile, než lidské oko? Je vybaven čtyřmi zrcadly, každé má průměr $8\,\jd{ m}$, expoziční doba pořizovaných snímků je $1000\,\jd{ s}$. Lidské oko shromažďuje světlo po dobu asi $0,2\,\jd{ s}$.
- Vymyslete jednoduchou metodu, kterou rozlišíte spojky od rozptylek s velkými ohniskovými vzdálenostmi ($>20\,\jd{ m}$), tj. že spojky nefungují jako lupa. Jediné pomůcky, které máte, jsou vaše oči, ruce, mozek a okolní zdi.
Nápověda: Sežeňte třeba brýlovou spojku a rozptylku a experimentujte.
2. Série 12. Ročníku - S. spektra, spektrografy a koutové odražeče
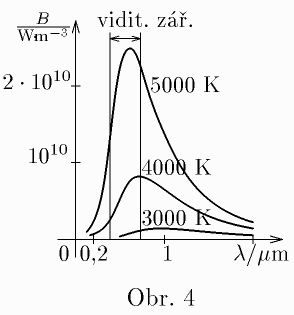
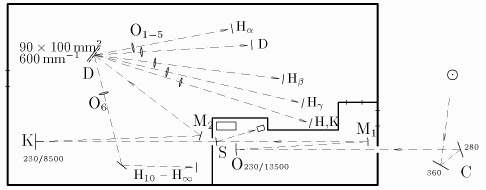
- Jak velký obraz Slunce se vytváří na štěrbině Ondřejovského spektrografu?
- Pokuste se přijít na důvod, proč se pro napájení spektrografu používají dvě zrcadla (coelostat), a nikoli jen jedno zrcadlo (heliostat).
- Jak dlouho čekali pozorovatelé na Zemi, než se jim vrátil signál vyslaný k Měsíci, který se na Měsíci odrazil od koutového odražeče?
- Dokažte, že tři na sebe navzájem kolmá zrcadla, použitá v koutovém odražeči, mají tu výhodnou vlastnost, že paprsek od nich odražený se šíří v přesně opačném směru, než přišel.
- Při noční jízdě automobilem pozorujeme na krajnici oranžové zářící předměty. Kde se bere energie na jejich „svícení“? Proč řidič nevidí ve zpětném zrcátku stejné svítící předměty?
3. Série 12. Ročníku - S. plachetnice a světlo
- Jaké zrychlení bude mít sluneční plachetnice o hmotnosti $m=10\,\jd{t}$ a velikosti plachet $S = 1000\,\jd{ m^{2}}$ nedaleko Země, kde je světelný výkon Slunce (solární konstanta) $k=1330\,\jd{W \cdot m^{-2}}$? Za jak dlouho by taková plachetnice dorazila od dráhy Země k dráze Marsu, pokud bychom ji vypustili s nulovou rychlostí? Předpokládejte, že velikost solární konstanty je v prostoru mezi Zemí a Marsem konstantní, zanedbejte gravitační vlivy všech těles. Poloměr dráhy Země je $1\,\jd{ AU}$, poloměr dráhy Marsu je $1,523\,\jd{ AU}$. $\jd{AU}$ je astronomická jednotka a její velikost je $1\,\jd{ AU}=1,495 978 70 \cdot 10^{11} \jd{m}$.
Velikost solární konstanty samozřejmě závisí na vzdálenosti od Slunce. Jaká je její velikost na Marsu?
- Vysvětlete proč je výhodnější vyrábět plachty sluneční plachetnice z materiálu, který má blízko k zrcadlovému lesku, než z matného materiálu.
- Jaká je intenzita elektrického pole (ve $\jd{V\cdot m^{-1}}$) v laserovém svazku s intenzitou $150\,\jd{ kW\cdot cm^{2}}$? Jak velká by musela být intenzita svazku, aby docházelo k ionizaci vzduchu?
- Jak by se musel upravit argument funkce kosinus, aby vztah
$$\textbf{E}(\textbf{r},t) = \textbf{E}_{0} \cos(ωt – k r + φ)$$
nepředstavoval rovinnou, ale kulovou vlnu. Kulová vlna je vlna, šířící se z bodového zdroje, asi jako když hodíte kámen do rybníka. Roviny konstantní fáze u kulové vlny jsou soustředné koule se středem ve zdroji.
4. Série 12. Ročníku - S. F-P rezonátor a lasery
- Představte si Fabry-Perotův rezonátor se vzdáleností jednotlivých odrazných ploch $d=3\;\mathrm{mm}$, vyrobený se skla o indexu lomu $n=1,5$. Pro jakou nejbližší vlnovou délku k $500\,\jd{ nm}$ dojde k maximální odrazivosti rezonátoru?
- Uvažujte F-P rezonátor z příkladu a), na nějž dopadá světlo kolmo. Kam se bude posouvat maximum z předchozího příkladu, jestliže budeme rezonátor postupně naklánět vůči směru paprsku o malý úhel $α$?
- Jakou teoreticky maximální účinnost přeměny čerpané energie lze dosáhnout u titan-safírového laseru, který svítí na vlnové délce $800\,\jd {nm}$, jestliže ho čerpáme argonovým laserem a použijeme čerpací vlnovou délku $515\,\jd{ nm}$.
- Jak daleko (ve frekvenční oblasti) jsou od sebe jednotlivé módy v argonovém laseru s laserovým rezonátorem o délce $1,5\,\jd{ m}$, resp. v polovodičovém laseru s délkou rezonátoru $0,3\,\jd{ mm}$. Většina plynů má index lomu blízký jedné, polovodiče mají index lomu poměrně velký, obvykle kolem $n\approx 3$.
5. Série 12. Ročníku - S. synchronizace módů (mode-locking)
Předpokládejme modově synchronizovaný laser s optickou délkou rezonátoru $l=1,8\;\mathrm{m}$, pracujícího na střední vlnové délce $λ=800\,\jd{nm}$ se středním výkonem $1\,\jd{ W}$.
- S jakou frekvencí laser produkuje jednotlivé pulsy? Jaká je mezi nimi prostorová vzdálenost?
- Jak je prostorově dlouhý puls o délce $70\,\jd {fs}$?
- Kolik fotonů je v jednom pulsu?
- Jaký je špičkový výkon v pulsu?
- Kolik módů potřebujeme k dosažení pulsů o délce $70\,\jd {fs}$? V jaké oblasti vlnových délek musí zesilovat aktivní prostředí? Předpokládejte stejnou amplitudu všech módů, které se účastní tvorby pulsu.
A protože tento díl seriálu byl předposlední soutěžní a vždy jsem se na něco ptal já vás, dám vám tentokrát možnost, abyste se zeptali vy. Napište mi s dalším řešením, co vás z optiky zajímá, co byste si rádi přečetli v posledním dílu seriálu, který vyjde až s řešením 5. a 6. série a už nebude obsahovat žádné úlohy. Pište prosím na zvláštní papír a výrazně jej označte „Co chci vědět z optiky“.
6. Série 12. Ročníku - S. optická vlákna
- Jak velká je vstupní numerická apertura u vlákna s gradientním indexem lomu $n=1,452$ a relativní změnou indexu lomu $Δ=0,01?$
- Jak dlouhý signál dostaneme na výstupu z optického vlákna s parametry z části a) o délce $100\,\jd {km}$, jestliže dáme na vstup signál dlouhý
$1\,\jd {µs}$? K výpočtům použijte nastíněného geometrického modelu.
- Jakou maximální přenosovou kapacitu (v bytech/s) můžeme na tomto vlákně provozovat? Předpokládejte, že přenesení jednoho bitu znamená přenést jeden impuls.