Series 4, Year 19
Upload deadline: -, CET
1. competition of balloons

This series of questions is dedicated to the research on the „planet of the balloons“.
This year balloons are competing in the 'The higher, the better' competition. Each balloon has a piece of string attached to measure his height. All balloons have the same parameters and noone of them have won yet.
The length density of string is 11 lufts per sprungl, density of atmosphere is 110101 lufts per cubic sprungl and the radius of each balloon is 10 sprungls and weight of balloon is 10 lufts. Every object in gravitation field of the planet increases its speed by 111 sprungls per temp. Calculate the maximum height which the referees will measure and how the balloon will move after reaching this height. Unlifted part of the string is laying freely on the ground. The competition happens at low altitudes, where density of atmosphere is approximately constant.
Hint: Sprungl, luft and temp are units used on planet of the balloons. Each balloon has maximum of 1 string attached.
Úlohu navrhl Petr Sýkora od Havránka.
2. expedition to the planet of the balloons
A big expedition to the planet of the balloons is being prepared. Preliminary data show following physical characteristics: the atmosphere consists of air of fly-weight 10001 lufts per fly and number of molecules in one fly is 10^{1101}, the thickness of atmosphere is 10^{10001} spurgles and by comparing of temperatures it was conducted that 7K on Earth corresponds to 1 luft times square spurgl per square temp.
Calculate temperature at the surface and decide if the astronauts should wear t-shirt or rather fur coat. The solution of IV.1 can help you.
Úloha ze starého ročníku FYKOSu.
3. balloons on the merry go round
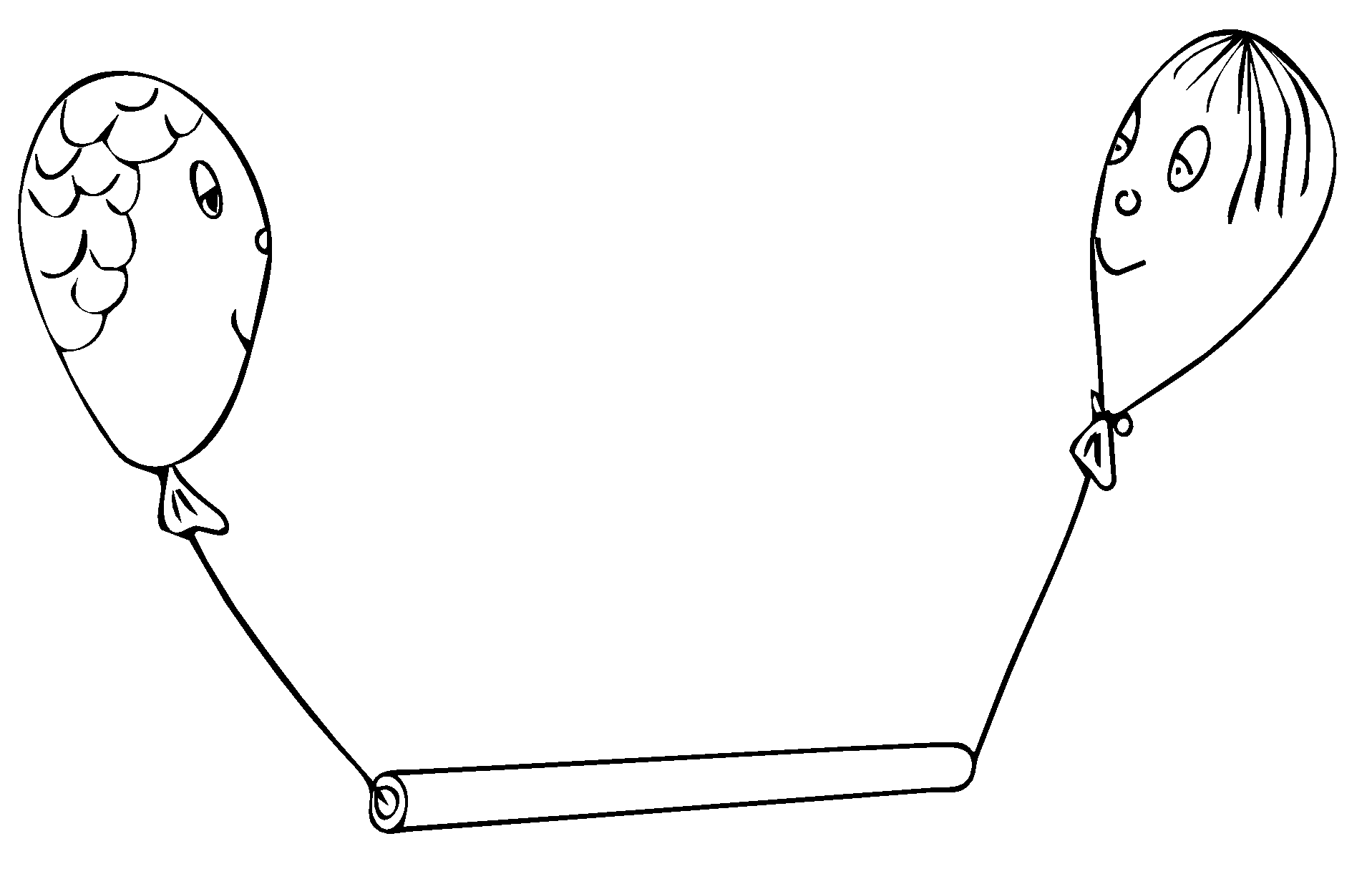
Two balloons are fixed on a single string of length $l$. The string is threaded through a horizontal hollow tube of length $L$. Both balloons weight approximately the same, however one is slightly heavier.
The tube starts spinning around vertical axis. What is the optimum position of this axis for the horizontal distance between balloons to be the biggest?
Vymyslel Jirka a Kájínek špatně pochopil.
4. wedding of two balloons
At the wedding ceremony the new couple kisses. For balloons it means to connect it orifices to connect the inside gas into a single One. Describe what would happened after the orifices are connected. Do not forget that all balloons have the same parameters.
Navrhl Petr Sýkora.
P. balloon-refugee

After a small revolution on planet of balloons one of balloons took refuge on Earth. First he was quarantined and his volume $V$ and temperature $T$ were measured.
However the immigration department decided that the balloon will not be freed until his volume is $V'$ and temperature $T'$. The balloon is not allowed to release or receive any heat or change the number of particles. What is the best way to reach required parameters and be released and live happy ever after on Earth?
Problém Matouš slyšel na přednášce prof. Koteckého a vymyslel řešení.
E. how the eyes are misleading

Balloons often assume that the constellation of stars close to the horizon look bigger then when located high at the sky.
Perform a measurement on the Earth and decide if it is really misleading observation. Measure angular distance $α(t_{1})$ of two selected stars which are approximately above each other and angular distance $β(t_{1})$ of other two stars at approximately the same height above horizon (i.e. independent check in two separate directions) at the moment, when the stars are as low above horizon as possible. Later on, find the same stars as high as possible and repeat the measurement recording $α(t_{2})$ and $β(t_{2})$ parameters. Try to measure with the highest precision.
We will specially recognise if you are able from known catalogued coordinates of stars calculate its theoretical angular distance. Do not forget to describe used equipment and discuss pros and cons. Plot schematic sketch of the sky around the stars and record time, direction etc. of the measurement. Finally estimate errors of measurement and discuss and compare the results.
Zformuloval Pavel Brom inspirován dotazem na hvězdárně.
S. fourth part
- What is the heat capacity of 3-atomic gas predicted by classical physics? The atoms are arranged in a triangular shape. To what capacity will it fall at 100K?
- Find out behaviour of the equations for internal crystal energy and energetic spectrum of black body radiation for low temperatures. Derive so called Wien's displacement law. It says that the frequency
ω_{m}, at which the spectral radiation of black body has its maximum is directly proportional to temperature.
- Build a better theory of heat capacity of crystals, to include collective vibrations of atoms. Do not calculate resulting difficult integrals.
Hint: There are sounds waves (longitudinal and transverzal at different speeds) propagating through crystal. Number of modes cannot be bigger than the degree of freedom 3N (N is number of atoms).
Zadal autor seriálu Matouš Ringel