Series 1, Year 24
Upload deadline: -, CET
1. floating sphere
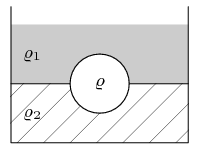
A solid sphere of density ρ is placed between two layers of immiscible liquids (see picture). Densities of the upper and lower liquids are ρ_{1} and ρ_{2} respectively. Assume that ρ_{1} ρ < ρ_{2}. Calculate the fraction of the sphere surrounded by the upper resp. lower liquid.
Z ruských bylin vyčetl Marek
2. sister planet
Many planets outside our solar system have been discovered during the past few years. It would be much more interesting, however, if we discovered a planet similar to the Earth. Assume that you want to find an Earth-like planet (radius close to that of the Earth) which orbits a sun-like star (similar mass and radius) once per terrestrial year. Assume that this system is about 10 pc away from the Sun. Find conditions which would allow you to observe the planet only by measuring the decrease in the star's luminosity and estimate how long will this decrease last. What would you do if the system contained more than one planet?
Po hvězdných dálavách zatoužil Karel
3. magical top

Jakub has a spinning top with a spiral drawn on its upper side. He lets the top spin and watch it from above. What does he see and why?
Na dětství zavzpomínal Jakub
4. rocking horse
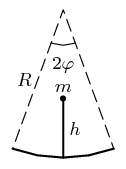
Massless rod of length $L$ is attached to an arch of top angle 2φ and radius $R$. A mass $m$ is glued to the rod's end (see picture). Assume that the body's motion is two-dimensional.
- Find the condition necessary for the system to be stable.
- What is the period of oscillations of the body about its equilibrium point?
P. to be, or not to be
Two travelers, one fat and the other skinny, are arguing who would have better chances of surviving in extreme conditions. Tell them who will live longer in the following environments. Hot(50 °C), cold(-1 °C), after a boat accident in the Mediterranean sea, inside a hurricane, inside a heavy snow storm and in the middle of earthquake inside a city. Except of their body fat they are exactly the same. They even wear the same clothes and they do not carry anything else. Be original and remember that details matter.
Ve známém televizním pořadu viděl Honza P.
E. shot put
We all know that in vacuum if we throw an object under a certain angle and with some initial speed the distance it will travel is independent upon the mass of the object. If we drop the vacuum assumption, the problem is not so simple. Experimentally find how does the distance of the point where the object hits the ground depends on its mass and shape. Make theoretical predictions (numerical calculations are allowed) and compare them with your findings.
S. complex warm-up
- Convince yourselves that the nth roots of a complex number of modulus one lie on a regular $n-gon$ and solve the Bombelli equation $x^{3}-15x-4$ = 0. (see the text for hints)
- Express the identities concerning sin(α+β) and cos(α+β) using the complex exponential.
- Show that we were allowed to neglect the higher powers in deriving the Bernoulli limit, i.e. show that it was legitimate to add the o(1/$N)$ term inside the parentheses.
- Use the little-o notation to solve the problem of small oscillations around equilibrium point in Yukawa potential $V$ = $k \exp(x/λ) /$ $x$.
- Prove that the Chebyshev polynomials cos($n$ arccos $x)$ are really polynomials.
Hint: Let's have a unit complex number $z$ with real part $x$. Then, the expression is equal to the real part of $z^{n}$.
Jakub Michálek a Lukáš Ledvina