Series 6, Year 22
Upload deadline: -, CET
1. resistance
Calculate the resistance of $n-dimensional$ cube between two most distant corners (with coordinates ( 0$,0,…,0)$ and ( 1$,1,…,1))$. The cube consists only from its edges (1-dimensional objects). Try to start with 3-dimensional cube and expand in higher dimensions.
Přednesl Lukáš Ledvina
2. escape from the charged sphere
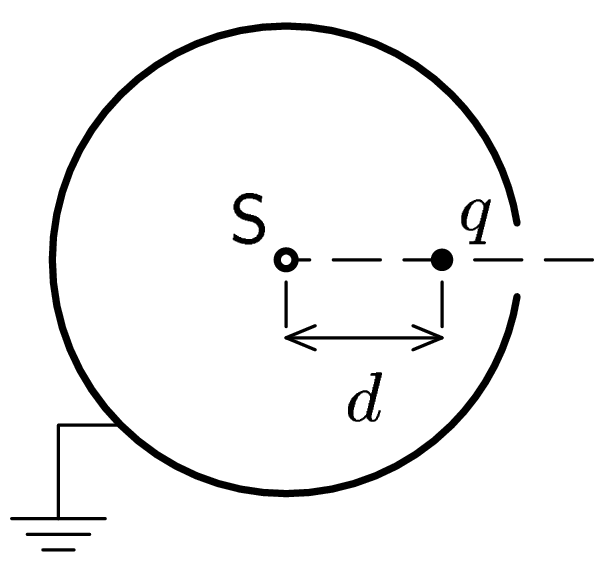
Inside of grounded conductive sphere is made a small orifice, just big enough for a small charged particle to pass through. Assume the particle is placed in distance $d$ from the center of the sphere (see picture).
The charged particle is set free. How far it will fly off from the sphere? Try to use method of mirror potential.
nad koulemi rozjímal Pavel M.
3. relativistic sphere
At the speeds close to speed of light you can observe contraction of objects. On the other hand the objects looks longer, then they are in reality (try to follow and compare light beams from closer and distant part of a body). Calculate, if these two effect will cancel for a sphere.
z Cambridge donesl Dalimil
4. stone on the piston
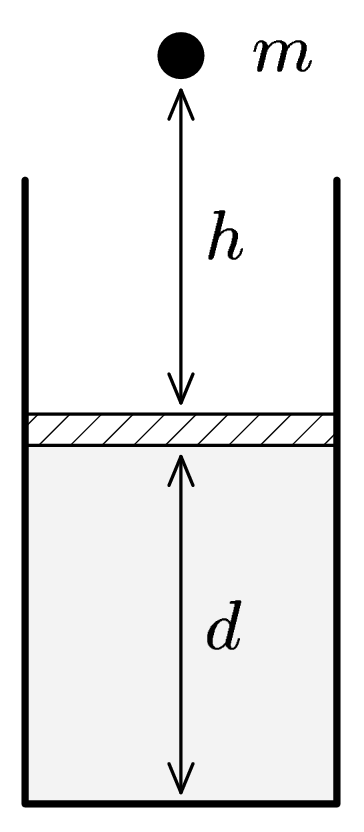
Marek has a piston of area $S$ filled with ideal gas in equilibrium ($p$, $V$ a $T)$. On this piston a stone falls down from the height $h$. Mass of stone is $m(see$ picture). Piston is pushed down and then comes up again and remains in a new position. How depends this new position on the mass of stone and the falling height? Is it possible for piston to become in equilibrium higher then the original position? How will change the temperature of gas?
vymyslel Mára po přednášce z termodynamiky
P. flying people
Titan (satellite of Saturn) is very cold (surface temperature is 94 K) with nitrogen atmosphere, with icy surface and hydrocarbon lakes on the surface. Radium of Titan is 5150 km, mass is 1 ⁄ 45 mass of the Earth, thickness if its atmosphere is 200 km and pressure on the surface is 1,5 bar.
Based on previous facts calculate acceleration due to gravity on the surface and estimate density of atmosphere. Comparing with parameters of birds at earth conditions decide, if feathered person could fly on Titan.
létat se zachtělo Honzovi P.
E. returnable flasks
Buy a standard glass bottle from bier of mineral water and find out, how the pitch of the tone depends on the water level inside the bottle, when you blow over the neck of the bottle.
vymysleli organizátoři na pravidelné schůzi
S. atomic models and Rutherford experiment
- Decide if the stability (e.g. dimensions) of Saturn model depends on atomic number $Z$.
- Change equation (12) for probability of scatter of $α-particle$ at high angle $φ$ in such way, to get more practical equation for probability of impact per unit area on scintillator. and show, how this can be used to get material of target. Further estimate how the equation would change when not considering the central charge $Ze$ but $Z$ spread elementary charges $e$ as is for example in Lenard model.
- In 1896 astronomer E. C. Pickering found in the spectrum of star $ζ$ Puppis lines, which fulfilled condition (7) for $n=2$ and $m=2,5;$ 3; 3,5; 4; 4,5;…,
e.g. also for half integers. Explain this inconsistency of Bohr model.
- ( Bonus: Find a dependence similar to equation (11) for Thompson pudding model and comment on differences. Or try to modify it in such way, that it considers all atoms in thin aluminium foil. Just play a little bit.
Na rozloučenou od autorů seriálu.