Series 6, Year 19
Upload deadline: -, CET
1. climbing a bump
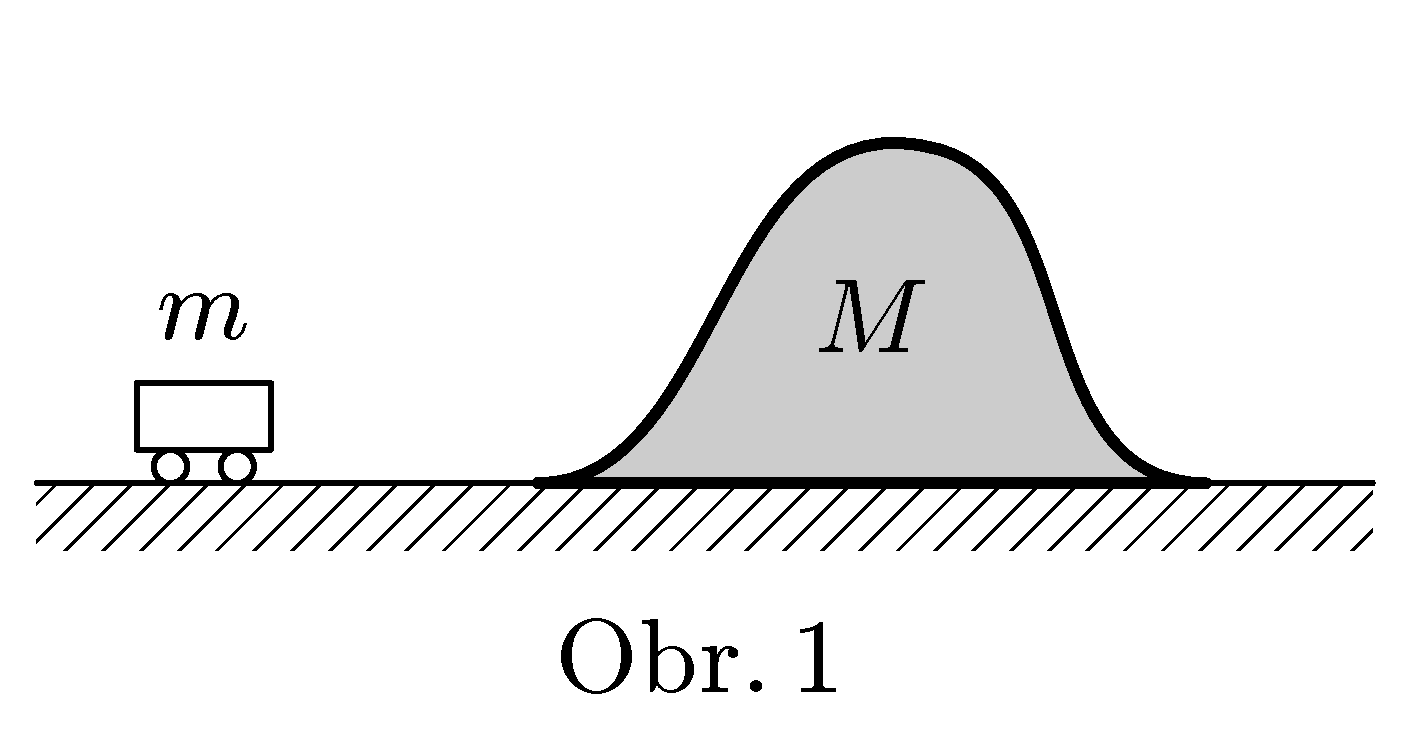
A carriage of mass $m$ travels in horizontal direction at speed $\textbf{v}$. In front of him is a „wooden bump“ of mass $M$ and height $h$, which slides on the horizontal plane without friction (figure 1). The carriage goes onto the bump. What conditions must be fulfilled for carriage to go over the bump? What will be the final velocity of the bump?
Našel Matouš v sovětské sbírce.
2. cuckoo-clock on the string
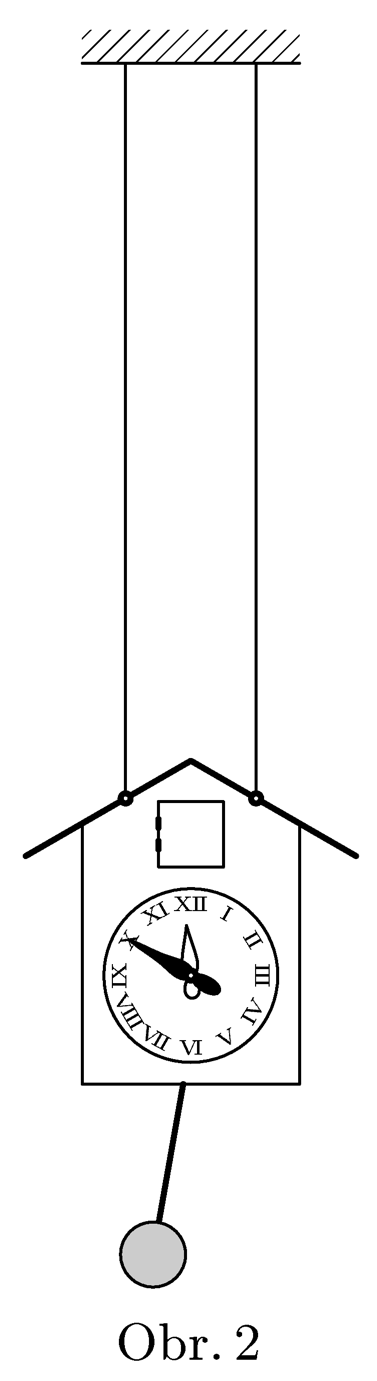
Cuckoo-clock of mass $M$ are fixed at two long parallel stings (figure 2). Pendulum consists of small mass $m$ and light rod of length $l$. Calculate, how much will such clock speed up comparing to the clock fixed on the wall.
Našel Matouš v sovětské sbírce.
3. spinning the electrical motor
On the axle of motor the sting is winded up. At the end of the string a small mass $m$ is fixed. If the motor is connected to the ideal voltage source of voltage $U$, small mass travels up at speed $v_{1}$. What speed will the small mass reach, if the voltage source is disconnected and the motor contacts are connected (shorted)? Assume friction-less devices.
Našel Matouš v sovětské sbírce.
4. Sun reflection
During sunny days we often experiment with square mirror giving reflections of Sun. Sometimes the reflection has LICHOBEZNIK shape, sometimes it is elliptical shape. What are the conditions for each case to happen? If possible, formulate your condition quantitatively.
Našel Matouš v sovětské sbírce.
P. strange boiling point
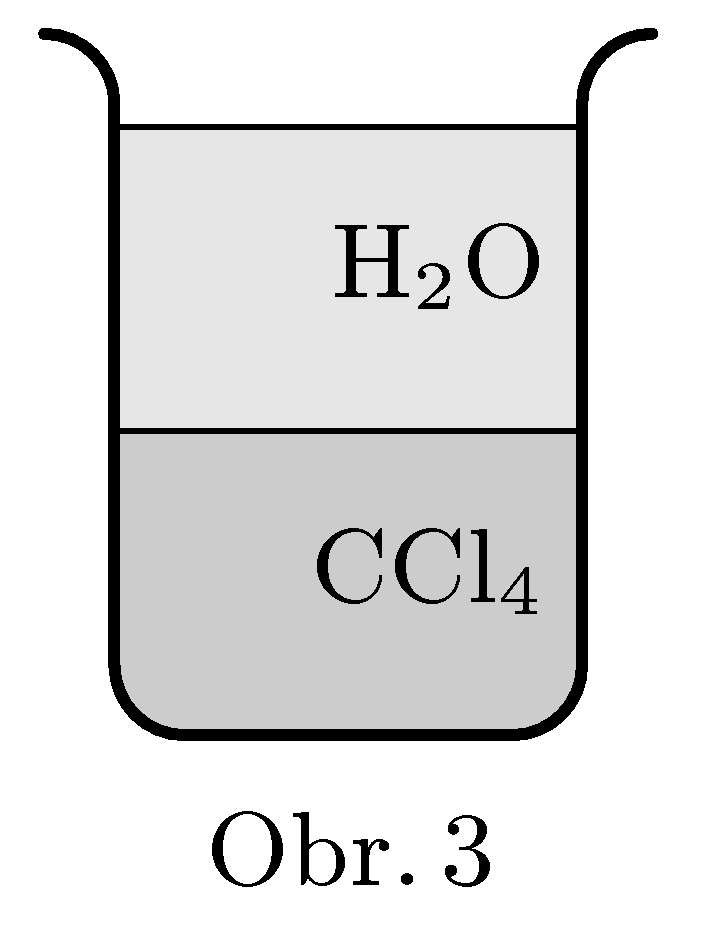
To the container is filled with two liquids – water and trichlormethan. These two liquids do not mix and boiling points are 100 °C and 77 °C for water and trichlormethan respectively. If this system is heated up, quite surprising observation can be made. The boiling (formation of bubbles) starts at around 66 °C. Explain such behaviour.
Našel Matouš v sovětské sbírce.
E. discover your body
As the last experimental question in this year (volume) we have following simple experiment. Chose two of you body fluids (saliva, blood, urine, sweat, tears, gastric juice) and measure at least one of its physical properties (density, viscosity, electrical conductivity, refractive index, boiling point). Follow the saying „The more is better“.
Tuto hovadskou úlohu vymysleli Jarda s Honzou po ICQ těsně před tiskem.
S. last question
- Describe qualitatively how the behavior of heat capacity of Ising model with zero external magnetic fields around critical temperature.
- Using similar approach, as we calculated behavior of magnetization $m$ in vicinity of critical point, calculate behavior of susceptibility $\chi (lim_{B\rightarrow0}\partial m⁄\partial$ B)$ and dependence of magnetization on magnetic field around critical temperature.
- Show, that the model of lattice gas gives condensation and find critical temperature.
- Investigate the model of binary alloy.
Zadal autor seriálu Matouš Ringel.