2. Série 23. Ročníku
Termín uploadu: -
1. kalamita
Jeden z organizátorů jel vlakem domů a zapadl ve vánici. Z dlouhé chvíle počítal sněhové vločky padající za oknem. A napadlo jej – kolik jich je asi v jednom kilogramu sněhu? Provedl kvalifikovaný odhad a spokojeně umrzl. Co mu vyšlo?
vzpomínáme na neznámého padlého
2. rušit krok
Jak rychle máme jít po visutém mostě, abychom jej co nejvíce rozkmitali? Úlohu vhodně parametrizujte a následně vyřešte.
Připomněl rotmistr Byrot.
3. brnkačka
Prodává se váleček, na kterém jsou malé výstupky. Váleček otáčeje se brnká o hranu ocelové destičky, která je nařezaná na proužky rozdílné délky. Ve skladbě na válečku se vyskytují všechny noty v daném neprázdném rozsahu (dejme tomu stupnice C dur). Dokážete zjistit tvar funkce konců nařezaných proužků?
navrhl hudební guru Jakub M.
4. Márovy pružiny
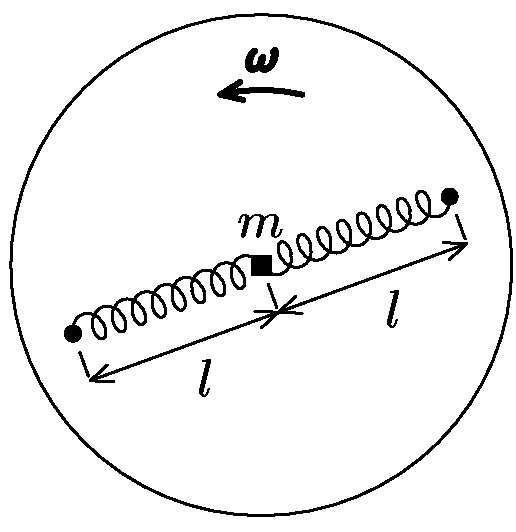
Kutil Mára si doma sestavil takovouto hračku: Na dřevěný kruh do jedné přímky procházející středem disku přimontoval dvě zarážky (stejně daleko od středu), mezi které na dvou pružinách o tuhosti $k$ napnul závaží o hmotnosti $m$. Závaží může bez tření klouzat po disku. Mára hračku položil na stůl a roztočil okolo osy disku úhlovou rychlostí $ω$, přičemž závaží mírně vychýlil z rovnovážné polohy. Kvalitativně popište pohyb závaží, a pokud si věříte, vypočítejte jej (za bonusové body).
aniž by viděl náboj na soustředění, vymyslel Mára
P. telekineze
Odkud bere magnet energii na zvedání věcí, když magnetická síla nemůže konat práci? Lorentzův vzorec $\vect{F} = q ( \vect{v}\times \vect{B})$ říká, že magnetická síla je kolmá na rychlost pohybujícího se náboje, a tedy pouze mění jeho směr hybnosti.
lámalo hlavu Honzovi Humplíkovi
E. metronom
Hrajete-li na hudební nástroj, určitě občas máte problémy udržet rytmus. Navrhněte experiment a změřte, jakou frekvenci (úderů o stůl, stisků klávesy, …) dokáže člověk nejlépe udržet. Existuje nějaká korelace mezi ní a jinými přirozeně se vyskytujícími jevy?
Parkinsonem onemocněl Honza Hermann
S. záhada meotaru a rybí oko
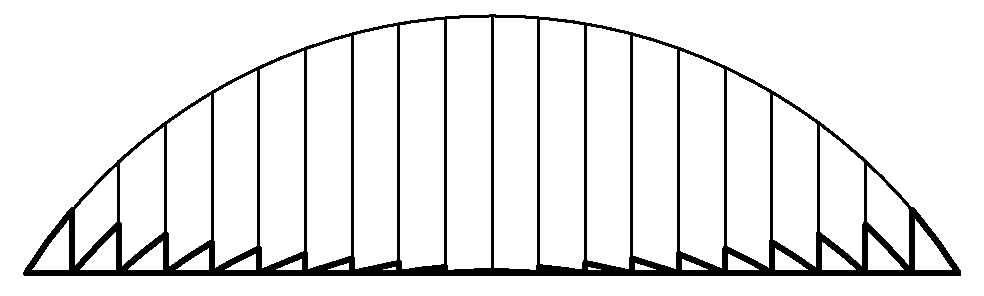
Možná jste si všimli, že mezi zdrojem a průhlednou podložkou na fólie je v tradičním meotaru za účelem soustředění světla vložená dost zvláštní čočka, která vypadá spíš jako rýhovaná deska (viz také úloha VI.2 ze XVII. ročníku). Vznikne tak, že standardní ploskovypuklou čočku rozřezáme na soustředné prstence, z každého si necháme jen úplný konec a výsledek opět složíme, takže získáme něco jako „osově symetrické pahorkaté sklo“ (viz obrázek).
Takto vzniklá čočka má všude stejný sklon jako původní spojka, a podle Snellova zákona tak očekáváme, že bude stejně dobře soustřeďovat světlo. Naproti tomu, z pohledu Fermatova principu, už každé dráze nepřísluší stejný čas, neboť jsme v různých místech odebrali různě tlusté vrstvy skla – například úplně nejkratší čas teď odpovídá cestě po optické ose. Zdá se tedy, že Fermatův pricnip selhává – podle něj by čočka soustřeďovala jen světlo jdoucí po optické ose a nefungovala tak, jak má. Rozhodněte kdo má pravdu: Snell, Fermat? A proč?
- Najděte dráhy paprsků ve dvojrozměrné situaci, kdy závislost indexu lomu na vzdálenosti $r$ od počátku je dána funkcí
$n(r)=n_{0}⁄(1+(r⁄a))$.
- Bonus: Vložíme-li do prostoru s proměnlivým indexem lomu bodový zdroj světla,
může se stát, že se velká část paprsků, které z něj vycházejí, sejde v jednom bodě, jako je tomu v případě spojné čočky. Takto vzniklý bod pak nazýváme obrazem bodu původního. Popište geometrické zobrazení $zdroj→obraz$, které tímto způsobem indukuje prostředí s indexem lomu z předchozí úlohy.
Z Kroniky Dalimilovy.