1. Série 7. Ročníku
Termín uploadu: -
1. neposedné válce
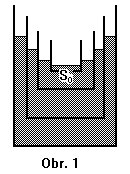
Velké množství dutých válců se zmenšujícími se průřezy je vnořeno do sebe a zalito vodou tak, že válec s menší plochou dna vždy plave ve válci, do kterého je vsazen (viz obr. 1). Nejmenší válec má plochu dna rovnu $S_{0}$, a ta je mnohem menší než plocha dna vnějšího válce. Vzdálenosti mezi dny jednotlivých válců jsou dostatečně velké, aby nikdy nedošlo k dotyku. Do nejmenšího válce přilijeme objem vody $V_{0}$. Po dolití opět válce v sobě plovou. O jakou vzdálenost a jakým směrem se posune dno nejmenšího válce vzhledem k nehybné podložce?
2. gramofonová přenoska
Raménko s gramofonovou přenoskou je uchyceno v čepu a vyváženo závažím. Pokuste se zdůvodnit proč je celá soustava uspořádána tímto způsobem. Navrhněte velikost a umístění závaží, je-li hmotnost přenosky 15 g, tuhost jehly ve vertikálním směru 80 N\cdot m^{−1} a její vzdálenost od čepu je asi 200 mm, víte-li, že maximální přípustná síla, jíž může jehla tlačit na desku je 0,02 N. Hmotnost ramena přenosky zanedbejte.
3. píst
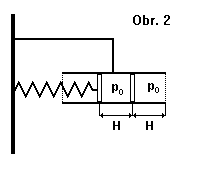
Ve vodorovně upevněné válcové trubici s otevřenými konci jsou umístěny dva písty ve vzdálenosti $H$ a $2H$ od pravého okraje válce (viz obr. 2). Levý píst je spojen s pružinou o tuhosti $k$ upevněnou ve stěně, pravý je volný. Na počátku je tlak na obou stranách pístů i mezi nimi stejný (roven $p_{0})$. Určete sílu, jakou musíme působit na pravý píst, vytáhneme-li ho k pravému okraji trubice. Hmotnost pístů můžete zanedbat.
4. korálek
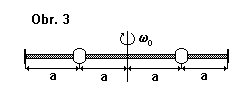
Na tyči zanedbatelné hmostnosti o celkové délce $4a$ jsou navlečeny ve vzdálenosti $a$ od osy otáčení dvě koule o hmotnosti $m$ (viz obr. 3). Na obou koncích tyče jsou umístěny dokonale pružné odrazné destičky. Tyč je roztočena na úhlovou rychlost $ω_{0}$, a poté jsou uvolněny obě koule. Za předpokladu, že se tyč nadále pohybuje volně a bez tření, určete:
- Po jaké trajektorii se budou pohybovat obě kuličky vzhledem k pozorovateli v inerciální soustavě.
- Jak se bude měnit úhlová rychlost soustavy $ω$ v závislosti na čase.
- Jak by se změnili výsledky předešlých úloh, kdybychom udržovali (např. pomocí motoru) úhlovou rychlost stále na hodnotě $ω_{0}?$
P. fošna
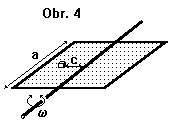
Čtvercová deska o straně délky $a$ (viz obr. 4) je upevněna na ose procházející jejím středem ve směru rovnoběžném s jednou ze stran. Ve vzdálenosti $c$ od této osy je na ní položeno malé tělísko hmotnosti $m$. Deska začne kmitat s nevelkou amplitudou kolem vodorovné polohy s frekvencí $ω$. Určete dobu (je mnohem větší než perioda kmitů), za kterou tělísko spadne z desky, je-li koeficient tření mezi deskou a tělískem $μ$.
S. relativita
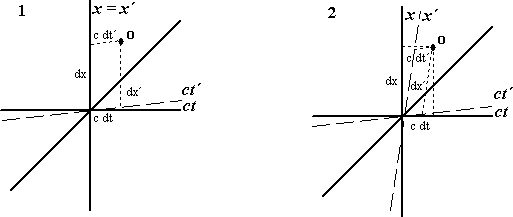
- Navrhněte postup (správný dle postulátů i a ii) synchronizace hodin.
- Všechny inerciální vztažné systémy jsou rovnocenné.
- Rychlost světla je ve všech soustavách stejná.
- Určete převod mezi souřadnicemi bodu O na diagramech 1 a 2, tj vztahy mezi d$x$ a d$x'$, resp. d$t$ a d$t'$, při dané rychlosti v (úseky d$x'$ a d$t'$ jsou rovnoběžné s osami $x'$ a $t'$, tlustá čára odpovídá rychlosti světla $c)$.