3. Série 9. Ročníku
Termín uploadu: -
1. vyhlodaný hranol
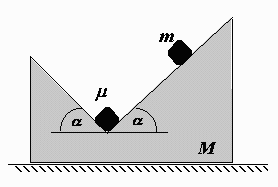
Na vodorovné rovině je položen vyhlodaný hranol o hmotnosti $M$ (viz obrázek), který se po ní může bez tření pohybovat. V nejnižším místě leží krychlička o hmotnosti $μ$. Na nakloněné části hranolu leží krychlička o hmotnosti $m$. I malé krychličky se mohou pohybovat po vyhlodaném hranolu bez tření. Jaká musí být splněna podmínka mezi hmotnostmi $M$, $m$, $μ$ a úhlem α, aby se po uvolnění krychličky $m$ krychlička $μ$ začala vůči hranolu $M$ pohybovat?
2. dálkový průzkum
Zjistit přesné údaje o Merkuru bylo pro astronomy vždy velkým problémem. Není jednoduché změřit pomocí dalekohledu jeho zdánlivý průměr, který nepřesahuje $13''$ a protože na povrchu Merkuru není vidět mnoho podrobností, zůstavala rychlost jeho rotace dlouho neznámá. Od konce minulého století se předpokládalo, že Merkur má takzvanou vázanou rotaci, to znamená, že jedna jeho otočka kolem osy je stejně dlouhá jako doba oběhu kolem Slunce, tedy 88 dní. Tento omyl vyvrátilo teprve v 60. letech radarové pozorování. Dejme tomu, že radioastronomové vyslali v čase $t_{0}=0\;\mathrm{s}$ signál směrem k Merkuru a jeho odraz pozorují od doby $t_{1}=1\,070{,}156\,24\;\mathrm{s}$ do $t_{2}=1\,070{,}188\,79\;\mathrm{s}$. Při dalším měření se soustředili na rudý posuv přijaté vlny. Původní signál měl frekvenci $100\;\textrm{MHz}$ a frekvence jednotlivých složek ozvěny se pohybovala od $f_{1}=99{,}977\,397\,00\;\mathrm{MHz}$ do $f_{2}=99{,}977\,405\,06\;\mathrm{MHz}$. Vypočtěte z těchto údajů (za předpokladu, že sklon rotační osy této planety vůči ekliptice je malý) vzdálenost a rychlost vzdalování Merkuru od observatoře, jeho poloměr, úhlovou rychlost rotace a dobu jedné otočky kolem osy.
3. Pinocciova čepička
Papa Karlo zhotovil pro Pinoccia čepičku z tenkého plechu ve tvaru kužele o výšce $20\;\textrm{cm}$ a s vrcholovým úhlem $60^\circ$. Bude ale takováto ozdoba držet na jeho hlavě, která má tvar koule o poloměru $15\;\textrm{cm}$ a je dokonale hladká?
4. lednička
V místnosti stojí otevřená lednička zapojená do zásuvky a mrazí. Po jedné hodině provozu necháme teplotu v místnosti ustálit. Jak se tato teplota liší od počáteční teploty v místnosti, pokládáme-li místnost za tepelně izolovanou?
P. vodní kyvadlo
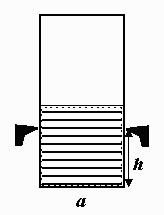
Mějme nádobu tvaru kvádru zanedbatelné hmotnosti o čtvercové podstavě strany $a$ a výšce $2a$. V této nádobě se nachází krychlové vodní těleso. V jaké maximální výšce $h$ ode dna můžeme naši nádobu zavěsit, aby se po zmrznutí vody převrátila? (Viz obrázek 2, který znázorňuje řez nádoby vertikální rovinou procházející těžištěm.) Uvažujte dva případy:
- nádoba je dokonale tuhá a voda zamrzá ode dna,
- voda si během zamrzání uchovává stále svůj krychlový tvar, nádoba je tedy dostatečně pružná. Přitom podél stěn led klouže, tedy výška závěsu nad podstavou zůstává konstantní.
E. gravitační zrychlení
Pokuste se změřit gravitační zrychlení co největším počtem metod. U každé metody proveďte 10–20 měření, porovnejte výsledky a přesnost různých metod.
Nápověda: Můžete využít matematického nebo fyzikálního kyvadla (těžký předmět na nehmotném závěsu). Při přímém měření, tedy zrychlení volného pádu, nepoužívejte lehké předměty (pírko), neházejte nic na hlavy chodců (špatně měřitelná výška). Ani vrhat své tělo vám nedoporučujeme (opakovatelnost pokusu). Při kutálení čehokoli po nakloněné rovině nezapomeňte uvážit, že těleso má i nějaký moment setrvačnosti. Lze použít i Adwoodův padostroj, rychlost výtoku kapaliny z nádoby nebo cokoliv jiného, co budete umět změřit.
S. střední volná dráha
Vypočtěte střední volnou dráhu molekuly dusíku při normálním tlaku a pokojové teplotě $t=20\;^\circ\mathrm{C}$. Poloměr molekuly dusíku $r=1{,}5\cdot 10^{-10}\;\textrm{m}$.