3. Série 2. Ročníku
Termín uploadu: -
1. skateboardista
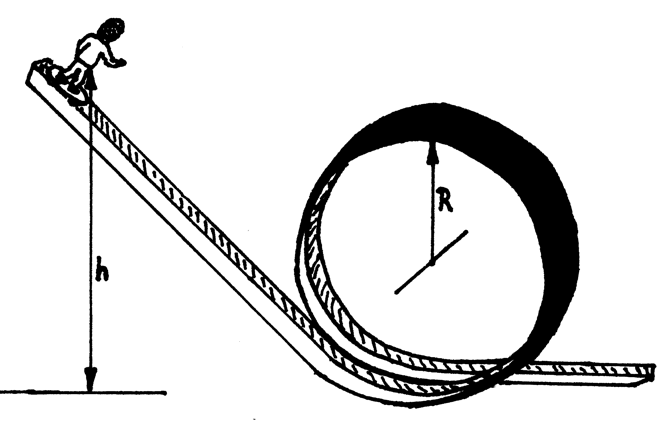
Skateboardista
Z jaké výšky se může pustit jezdec na skateboardu po dráze na obrázku, aby to nebylo zdraví škodlivé?
2. klubíčko
Klubíčko s koncem připeněným k začátku nakoněné roviny se kutálí bez tření s podložkou a přitom se rozmotává. Co se při tom děje s energií klubíčka?
3. síla přitažlivosti
Kdyby celý prostor byl prázdný mimo dvou kapek vody, budou se tyto kapky přitahovat podle Newtonova gravitačního zákona. Nyní předpokládejme, že celý prostor je vyplněný vodou s výjimkou dvou bublin (obrázek). Jak se bubliny budou pohybovat?
4. jak hluboká je studna?
Hloubku studny chceme určit s relativní chybou $2\; \%$ tak, že do ní pustíme kámen a měříme dobu, za kterou uslyšíme pád kamene na dno od jeho vypuštění. Při jaké hloubce studny už musíme uvažovat rychlost šíření zvuku?
E. index lomu
Určete co nejpřesněji index lomu přiloženého plátku umělé hmoty. Uveďte postup a odhadněte přesnost provedeného měření.
S. zeměměřiči podruhé
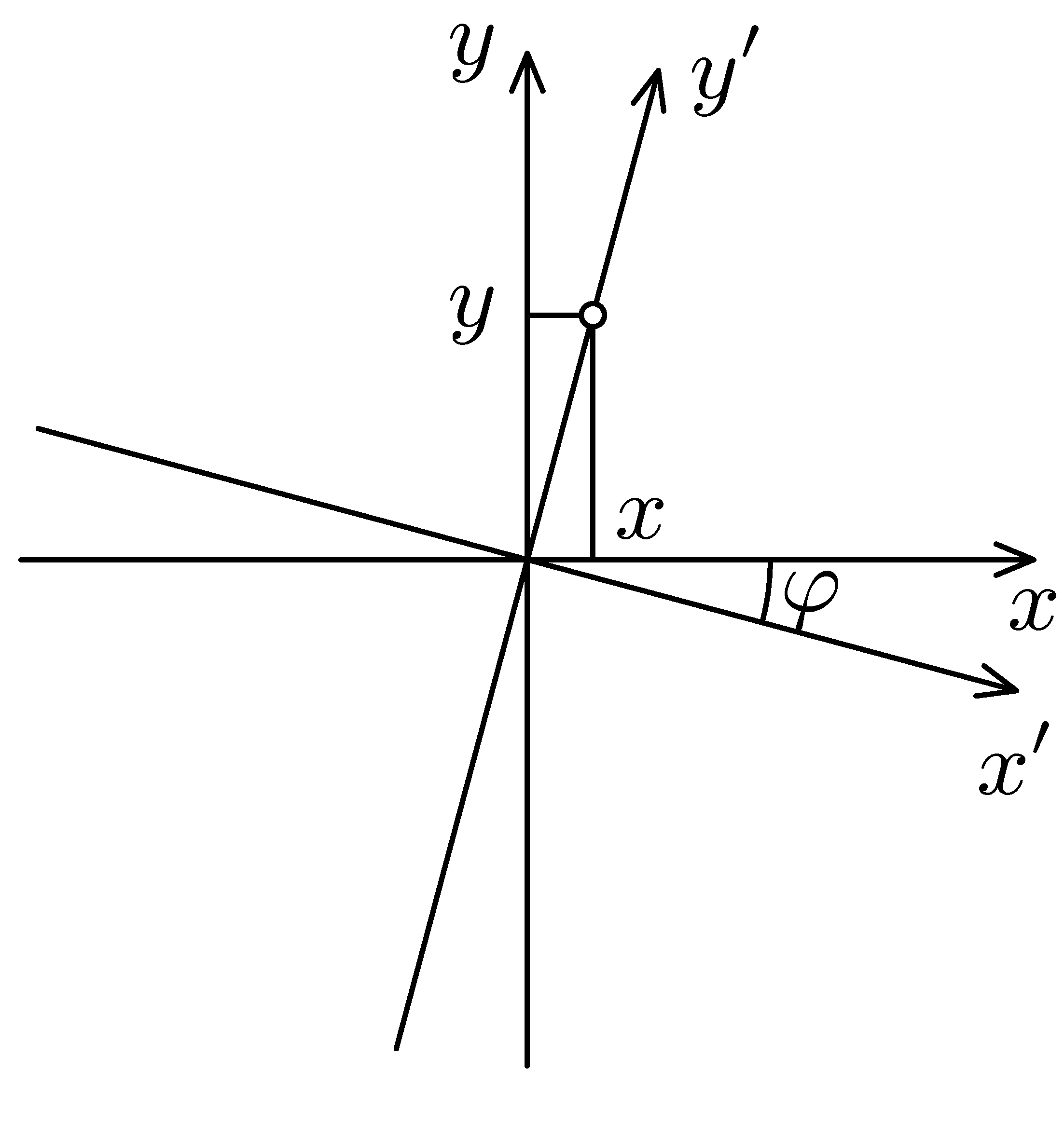
- Vraťme se opět do Severního království. V řešení příkladu I.S jste velkým zeměměřičům správně poradili převodní vzorce
$$x′=x\cos φ-yk\sin φ\; (1)$$ $$y′=kx\sin φ+y\cos φ\; (2)$$
kde $k$ je poměr metr ku severské míli a $φ$ úhel mezi magnetickým pólem a Severkou. Zeměřičům se však tento výsledek moc nelíbil, a to hned ze dvou důvodů – za prvé se v nich proti všem tradicím převádí severská míle na metr, s čímž se ale budou muset vyrovnat sami, ale hlavně za druhé neměří v Severním královstní odchylku mezi oběma používanými severními směry pomocí úhlu, ale pomocí tzv. odklonu $u$. Odklon osy $y′$ od osy $y$ je definován jako $u=x/y$, kde $x$ a $y$ jsou souřadnice bodu, který leží ve směru Severky, tj. osy $y$. Ukažte, že odklon $u$ nezávisí na tom, který bod na ose $y′$ v definici zvolíme, že odklon osy $y$ od $y′$ je $u$ a vyjádřete převodní vztahy (1) a (2) v závislosti na odklonu místo na úhlu.
- Zeměměřiči při porovnání svých výsledků zjistili zajímavou věc. Většina údajů se vlivem používání odlišných severních směrů liší, ale jeden údaj, který získávají podle vzorce $Δx+(kΔy)$, resp. $Δx′+(kΔy′)$, vychází oběma zeměměřičům stejně. Je to náhoda? Pokud ne, tak to dokažte a odůvodněte proč.