6. Série 18. Ročníku
Termín uploadu: -
1. fotoefekt
Na katodu fotočlánku dopadá ze rtuťové výbojky světlo o vlnové délce $546,1\, \jd{nm}$ a k potlačení proudu vznikajícího díky fotoelektrickému jevu je potřeba napětí $U_{1}=1,563\,\jd{V}$. Dopadá-li na katodu světlo o vlnové délce $404,7\, \jd{nm}$, je potřeba napětí $U_{2}=2,356\, \jd{V}$. Vypočítejte hodnotu Planckovy konstanty $h$.
Našel Honza Prachař v jedné sbírce.
2. jak vyrobit černou díru
Pokud stlačíme hvězdu (či jakékoliv jiné těleso) na kouli o poloměru $r_{g}$, zhroutí se nenávratně do černé díry. Tzv. Schwarzschildův poloměr $r_{g}$ si lze v klasické analogii představit jako poloměr tělesa o hmotnosti $M$, z jehož povrchu lze uniknout pouze rychlostí světla (úniková rychlost je $c$).
Na základě znalosti hmotnosti hvězdy $M$ určete Schwarzschildův poloměr $r_{g}$ a kritickou hustotu hvězdy $ρ$, při které se přemění v černou díru. Příklad řešte obecně a poté konkrétně pro Zemi, Slunce a jádro galaxie o hmotnosti 100 miliard Sluncí.
Jarda
3. sonda NASA
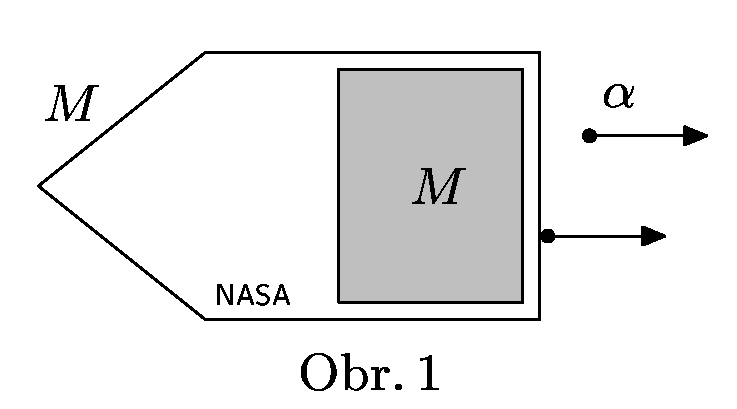
Jet Propulsion Laboratory v Kalifornii vyvíjí pro NASA nový typ raketových pohonů. Pohonná jednotka využívá hybnost $α$-částic při rozpadu nuklidu fermia $^{257}_{100}Fm_{157}$, jehož hmotnost je $m_{Fm}$ a poločas rozpadu $T$. Druhým produktem přeměny je nuklid kalifornia $^{253}_{98}{Cf}_{155}$. Hmotnost $α$-částice je $m_{α}$, hmotnost nuklidu kalifornia je $m_{Cf}$, přeměnou se uvolní energie $E$. Předpokládejte, že každá $α$-částice opouští raketu ve stejném směru.
Vesmírná sonda s popsaným pohonem je na počátku v klidu, její hmotnost je $M$, hmotnost pohonné látky je také $M$. Určete rychlost sondy $v$ po přeměně poloviny hmotnosti nuklidů fermia. Výslednou hodnotu dopočítejte i číselně pro hodnoty $E = 1,106\cdot 10^{-12}\, \jd{J}$, $M = 4\, \jd{kg}$ a $T = 100,5\, \jd{dní}$, ostatní hodnoty najdete v tabulkách.
SR olympiáda.
4. nezastavitelný chodec
Vraťte se na chvíli do Atén na loňské olympijské hry a určete, jaká je teoretická maximální rychlost chodce. Chodec nebude diskvalifikován, pokud se každý rozhodčí (pozorovatel) shodne na tom, že alespoň jedna noha chodce stojí v každém okamžiku na zemi.
Kdo jiný, než Matouš.
P. výlet na Stonehenge
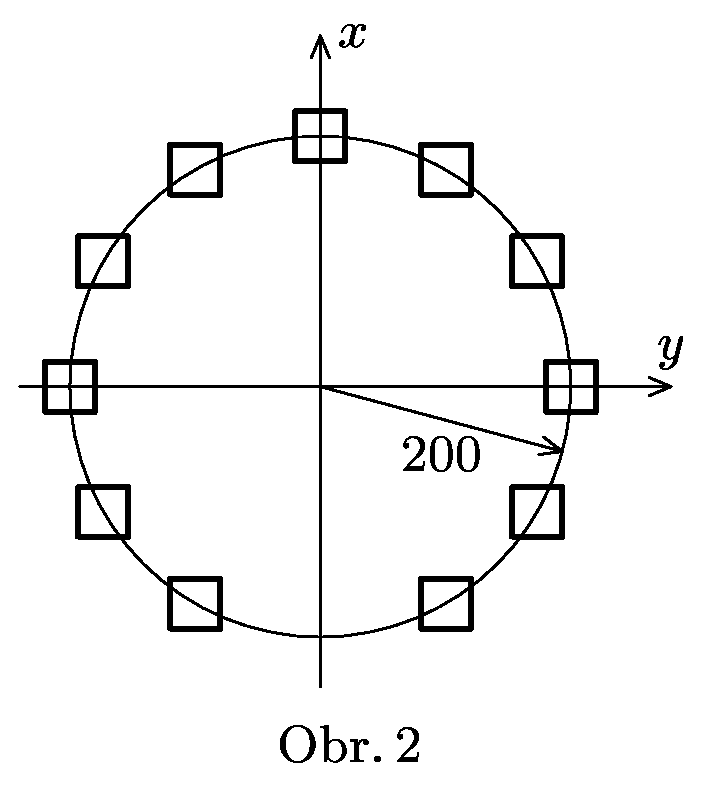
Představte si, že v raketě prolétáváte nad Stonehenge. Ten je tvořen kameny ve tvaru kvádrů rozmístěných do vrcholů pravidelného dvanáctiúhelníku (viz obrázek 2) o poloměru $200$. Letíte nad osou $x$ ve výšce $z=50$ a díváte se vodorovným směrem. Když jste v bodě o souřadnicích ($-200$, $0$), resp. ($0$, $0$), uvidíte svět přesně tak, jak je zobrazen na obrázku 6, přičemž oba máte shodné oči (tzn. např. stejný zorný úhel). Z obrázků přibližně určete poměr rychlosti rakety a rychlosti světla.
Matouš.
E. chyťte foton
Změřte rychlost světla ve vakuu. Provést to můžete libovolným způsobem, použijte třeba i mikrovlnnou troubu.
Co jiného dát jako experiment do roku fyziky.
S. Hamiltonův formalismus
Langrangián částice v elektromagnetickém poli je $L=\frac{1}{2}mv-qφ+q v\cdot A=\frac{1}{2}m\cdot \sum_{i=1}^{3}v_{i}-qφ+q\cdot \sum_{i=1}^{3}v_{i}A_{i}$,
kde $φ$ je elektrický potenciál a $A$ magnetický vektorový potenciál.
- Určete zobecněné hybnosti částice $p_{i}$ příslušející rychlostem $v_{i}$.
- Napište Hamiltonovu funkci (v proměnných ($x_{i}$, p$_{i})!)$.
- Řešte Hamiltonovy rovnice, je-li $A=0$ a $φ=-Ex_{1}$.
Zadal Honza Prachař.