2. Série 22. Ročníku
Termín uploadu: -
1. duhová energie
Kde a kdy na Zemi nelze vidět duhu?
na schůzce vypotil Aleš
2. odhalte tajemství šuplery
Vysvětlete nám, jak funguje „šuplera“, že dokáže měřit desetiny milimetru.
nad tajemstvími života se zamyslel Marek Scholz
3. ledvinové koule
Malá koule stojí v klidu na velké kouli, která volně leží na podložce. Do malé koule nepatrně strčíme a ta se svalí na zem. Jak daleko od původního bodu dotyku velké koule se zemí malá koule dopadne?
na teoretické mechanice zkoulel Lukáš Ledvina
4. do nekonečna a ještě dál
Bohatý vesmírný turista si zaplatil výlet do hlubokého vesmíru. Raketa vyletí ze Země a rovnoměrně zrychluje se zrychlením $a$, což si turista může ověřit například pouštěním míčku. Nudnou cestu si krátí zíráním ze zadního okénka, pozorováním Země. Po nějaké době (Jaké? Aspoň řádový odhad.) se mu začne zdát, že něco není v pořádku – Země se pomalu přestává zmenšovat. Z toho usoudí, že raketa zpomaluje, což neodpovídá tomu, že raketa stále má zrychlení $a$. To ale turistu nenapadne a rozlobeně jde za kapitánem požadovat vysvětlení. Co mu kapitán řekne?
Předpokládáme, že turista vidí celé elektromagnetické spektrum a má železné nervy a pozorování vydrží.
o prázdninách zkoušel Marek Pechal
P. milenecká
Jak se změní teplota pod peřinou, pokud jsou pod ní dva lidé místo jednoho?
vymyslel zmrzlý milovník Honza P.
E. šikmá věc
Kolik vody musí být v PET lahvi postavené na uzávěr, aby její stabilita byla největší (při vychýlení ze svislé polohy spadne ze nejdelší čas)? Nezapomeňte na teoretickou předpověď.
nad vypitou lahví se zamyslel Béda
S. Young a vlnová povaha světla
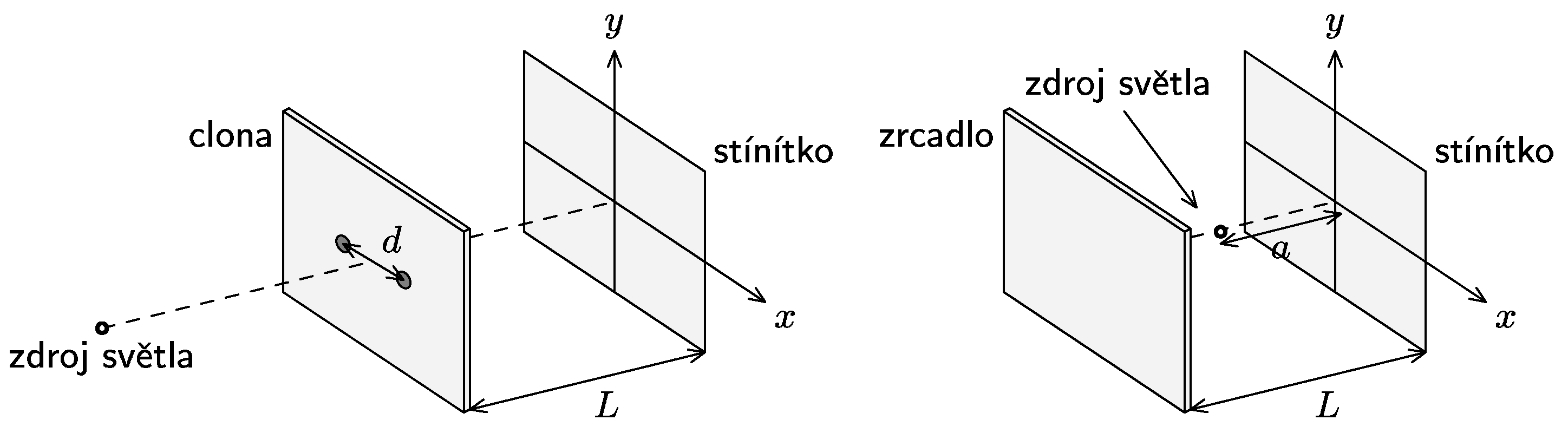
K zadání úlohy
- Jaký tvar interferenčních proužků na stínítku byste očekávali v následujících dvou sestavách? Najděte rovnice křivek maximální intenzity a zkuste jich několik načrtnout.
- Ukažte, jak by dopadl Youngův experiment, jestliže by se světlo chovalo podle Newtonových představ (tzn. difrakce ano, interference ne). nezapomeňte vzít v úvahu různý úhel dopadu světla na různá místa stínítka.
- Užitím vyloženého kvantověmechanického popisu určete rozložení intenzity, jaké by dostal Jöhnsson při použití čtyřštěrbiny (tedy čtyř úzkých rovnoběžných otvorů rozmístěných ve vzdálenostech $b$ od sebe). Načrtněte reprezentativní úsek grafu a okomentujte přednosti většího počtu otvorů.
Autoři seriálu