4. Série 23. Ročníku
Termín uploadu: -
1. modrá nebo zelená?
Hlavním zdrojem atmosférického kyslíku jsou fotosyntetizující rostliny. Představte si, že dojde k jejich masovému vymření. Na jak dlouho vystačí světové zásoby kyslíku, předpokládáme-li, že lidstvo a zbytek planety nijak nezmění svou spotřebu. Potřebné údaje určitě najdete na internetu.
při čtení levného sci-fi napadlo Aleše
2. horečka
Janap šla domů z hvězdárny a při pohledu na východ Slunce ji napadlo, jak by asi jednoduše šla spočítat jeho teplota. Prozradíme vám, že Země je absolutně černé těleso s teplotou $0\, \jd{^{o}C}$.
na přednášce ze statistické fyziky řešila Janap
3. smrtící kolotoč
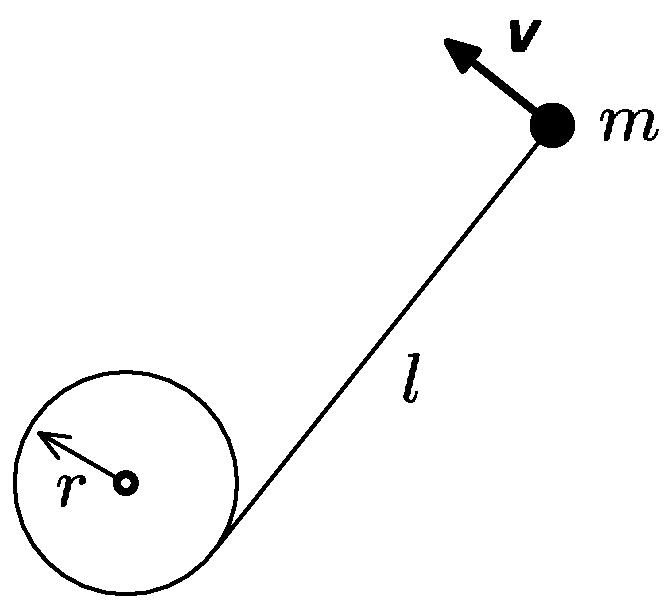
Na kůl o poloměru $r$ zabodený do země je lanem délky $l$ přivázané závaží hmotnosti $m$. Lano je napnuté a závaží leží na zemi. Lukáš se rozběhne a nakopne závaží kolmo na lano tak, že bude mít rychlost $v$. Lano se po tomto rázu začne navíjet na kůl. Spočítejte, jak se musí měnit koeficient smykového tření mezi závažím a zemí v závislosti na vzdálenosti od kůlu, aby při navíjení zůstala rychlost závaží konstantní.
po lunaparku zatoužil Lukáš L.
4. Terka skáče
Terka skáče z metrové zídky. Na začátku má ruce natažené zvednuté nad hlavu, během pádu ruce ale spouští. O kolik takto zmenší svou rychlost při dopadu? Kvalifikovaně odhadněte hmotnost, zrychlení a rychlost Terčiných rukou, jakožto i další potřebné parametry jejího těla, a úlohu vyřešte.
honilo se hlavou Terce při seskoku padákem
P. úleva u ohradníku
Zamyslete se nad tím, jak je to s odporem tekoucího elektrolytu. Je jeho velikost závislá na tom, jestli teče po směru elektrického proudu v něm, nebo naopak? Zkuste odhadnout rozdíl, je-li.
ránu dostal Grepe
E. MacGyver a teploměr
Z materiálů, které máte doma k dispozici, zkonstruujte funkční teploměr a pomocí vhodných známých teplot nakalibrujte jeho stupnici. Nezapomeňte nám poslat fotografii výsledku vašeho snažení.
Parkinsonem onemocněl Honza Hermann
S. maxwellobraní
- Co se stane, když do krystalu kalcitu kolmo posvítíme kruhově polarizovaným světlem?
- Představte si, že je právě čas $t=0$, široko daleko není žádný náboj
($ρ=\textbf{j}=0)$, a my známe počáteční elektromagnetické pole v celém prostoru $\textbf{E}(\textbf{r},0)$ a $\textbf{B}(\textbf{r},0)$. Z rovnic (14) a (15) tedy můžeme vyjádřit časové derivace $∂\textbf{B}⁄∂t$ a $∂\textbf{E}⁄∂t$ pomocí prostorových a vypočítat tak $\textbf{E}$ a $\textbf{B}$ v následujícím okamžiku. Tento postup můžeme iterativně opakovat a dostat tak celý časový vývoj pole pro $t>0$. Jak je možné, že vůbec nemusíme použít první a druhou Maxwellovu rovnici?
- Uvažujte náboj velikosti $q$, který je v klidu pro $t\lt0$, a v čase $t=0$ na něj začne dopadat rovinná světelná vlna. Jak se bude náboj následně pohybovat, když světlo je polarizované (i) lineárně (ii) kruhově? Promyslete nejprve kvalitativně, přesný výpočet, případně počítačová simulace obdrží bonus.
Vyrobily MD-závody-s-časem.