2. Série 9. Ročníku
Termín uploadu: -
1. Nezbedkova Nezbedka
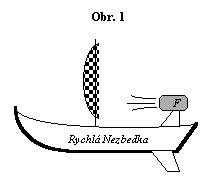
Na obrázku 1 plove loďka. Její majitel, známý vynálezce a kutil Nezbeda, vyřešil problém bezvětrného počasí následujícím způsobem: na záď lodi připevnil výkonný fén značky Fukar a nasměroval jej vpřed přímo na malou lodní plachtu. Na vás teď je, abyste usoudili, za jakých podmínek se loďka rozjede vpřed či vzad. Můžete se také zamyslet nad tím, jaké zlepšovací návrhy byste Nezbedovi poradili, aby jeho pohon pracoval za bezvětří co nejefektivněji.
2. nukleony
Spočtěte střední vzdálenost mezi nukleony v jádře. Zadány máte hmotnosti těchto částic:
| jádro | neutron | proton | deuterium | tritium | helium |
| hmotnost $\left[10^{–27}\;\textrm{kg}\right]$ | $1{,}674\,929$ | $1{,}672\,623$ | $3{,}343\,590$ | $5{,}008\,271$ | $5{,}008\,239$ |
Poznámka: Silná interakce je invariantní vůči záměně protonů a neutronů v jádře. Také platí, že na vzdálenostech $10^{–15}\;\textrm{m}$ jsou jaderné síly daleko intenzivnější než elektromagnetické působení.
3. válcovací stolice
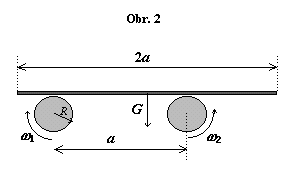
Dva stejné válce o poloměru $R$, jejichž osy jsou rovnoběžné a leží ve vodorovné rovině ve vzdálenosti $a$, rotují opačnými směry. Na tyto válce položíme vodorovně desku délky $2a$ o hmotnosti $m$ tak, že přečnívá vpravo více než vlevo (viz obr. 2). Mezi deskou a válcem působí tření s koeficientem $μ$. Co se bude dít s deskou,
- pokud jsou obvodové rychlosti stejně veliké,
- pokud je obvodová rychlost levého válce dvakrát větší než obvodová rychlost pravého?
4. elektrická krychle
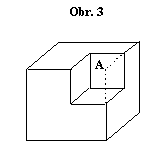
Představme si krychli s rovnoměrně rozloženým nábojem o hustotě $r$ v celém jejím objemu. Ve vrcholu $A$ jsme naměřili intenzitu elektrického pole $\textbf{E}$. Jakou intenzitu naměříme v bodě $A$, jestliže vyřízneme z krychle krychličku o poloviční délce hrany, jak je znázorněno na obr. 3?
P. Lomonosův průvan
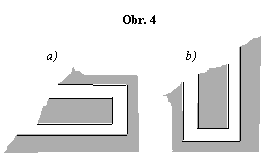
Velký přírodovědec M. V. Lomonosov studoval ve své světově proslulé práci „O volném pohybu vzduchu v dolech“ závislost směru proudění vzduchu na ročním období. Po dlouhém a strastiplném bádání dospěl k závěru, že teplota vzduchu je v dole stále stejná po celý rok. (V jeho době byly doly ještě poměrně mělké.) Určete, jakými směry bude vzduch proudit v létě a v zimě v dolech umístěných podle obr. 4.
E. odpolední čajíček
Pokuste se změřit odpor spirály elektrického vařiče.
Návod: Ohřívejte vodu vařičem a sledujte závislost její teploty na čase. Z této závislosti zjistěte výkon vařiče, ze kterého už snadno naleznete odpor spirály. Zřejmě vám už došlo, že tato úloha je takzvaně experimentální.
S. Mayerův vztah
Jde o úlohu jednoduchou, ale pokud ji budete chtít řešit, radši si ještě jednou přečtěte text seriálu (i když vás možná trochu nudí) a pokud příklad zdárně vyřešíte, určitě pochopíte, o co v tomto díle seriálu šlo. Tedy:
Odvoďte, jak vypadá 1. věta termodynamická pro izochorický děj ($V=\;\mathrm{konst})$ a určete tím, co znamená výraz $c_{v}=1/n\cdot dU/dT$.
Výsledek po dosazení do jedné z výše uvedených rovnic (snadno naleznete které), nazýváme Mayerovým vztahem.