6. Série 19. Ročníku
Termín uploadu: -
1. zdolání kopečku
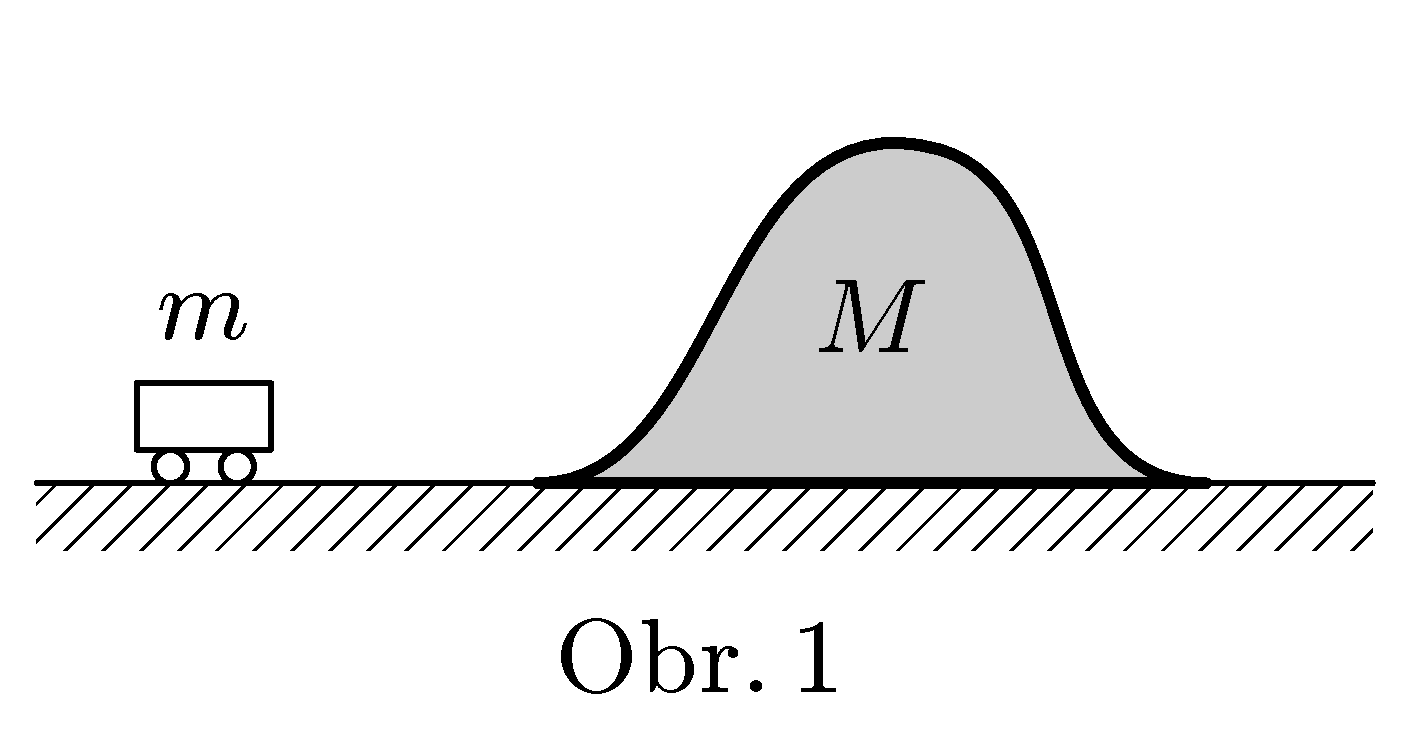
Vozíček o hmotnosti $m$ jede po rovině rychlostí $v$, na níž leží dřevěný „kopeček“ o hmotnosti $M$ a výšce $h$, jenž po rovině klouže bez tření (viz obr. 1). Vozíček na kopeček najede. Za jakých podmínek se mu podaří přejet přes vrchol? Jakou rychlostí se bude hora nakonec pohybovat?
Našel Matouš v sovětské sbírce.
2. kukačky na lanech
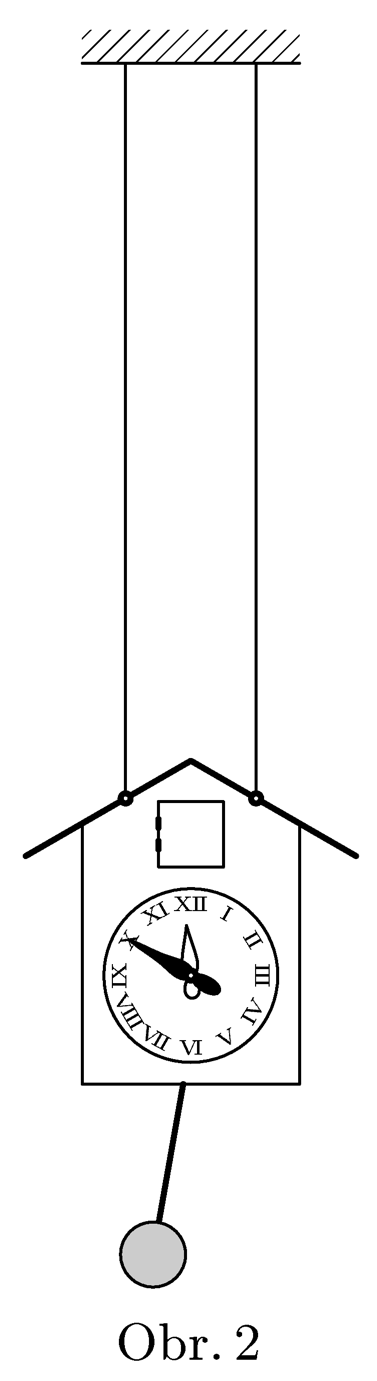
Kyvadlové hodiny o hmotnosti $M$ jsou zavěšeny na dvou dlouhých rovnoběžných lanech (viz obr. 2). Kyvadlo se skládá ze závažíčka o hmotnosti $m$ a lehké tyčky o délce $l$. Určete, o kolik se budou takové hodiny předbíhat (opožďovat) oproti hodinám pevně přibitým na stěně.
Našel Matouš v sovětské sbírce.
3. roztáčíme elektromotor
Na hřídeli elektromotoru je navinuta nit, na konci které je zavěšeno závaží o hmotnosti $m$. Pokud motor připojíme na ideální zdroj napětí $U$, závaží pojede vzhůru rychlostí $v_{1}$. Jakou rychlostí bude závaží klesat, pokud zdroj odpojíme a vstup elektromotoru zkratujeme? Mechanické tření neuvažujte.
Našel Matouš v sovětské sbírce.
4. sluneční prasátko
Za slunečných dní je oblíbenou zábavou vrhat obdélníkovým zrcátkem sluneční prasátka. Možná jste si všimli, že někdy má prasátko lichoběžníkový tvar a jindy tvar elipsy. Za jakých okolností nastává každá varianta? Pokud možno svou podmínku zformulujte kvantitativně.
Našel Matouš v sovětské sbírce.
P. podivný bod varu
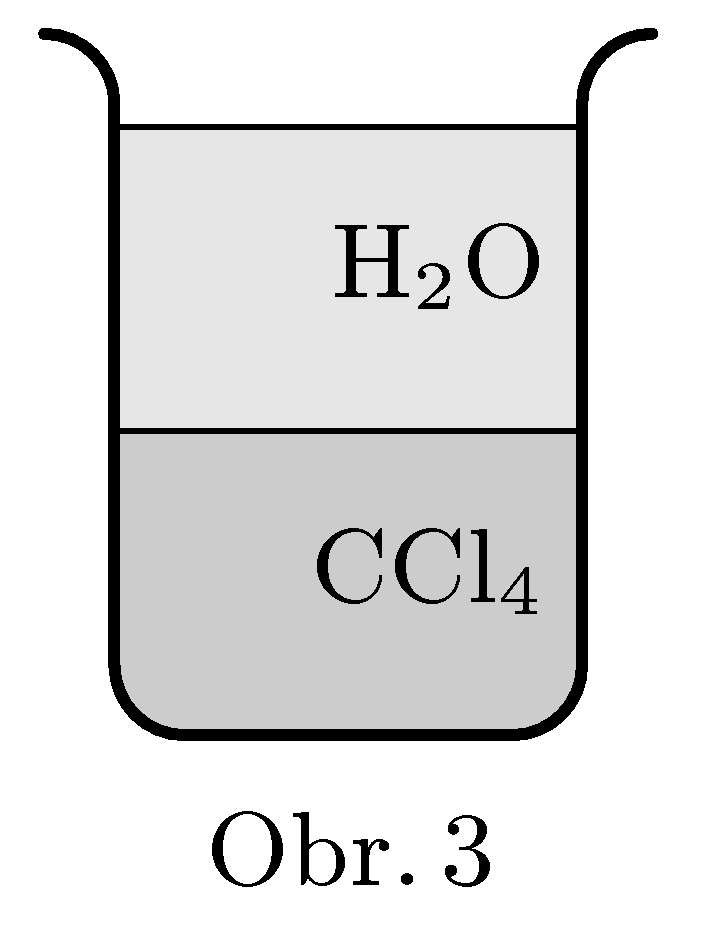
Do nádoby nalijeme dvě kapaliny, vodu a tetrachlormetan. Tyto dvě kapaliny se mezi sebou nemísí. Teplota varu vody je 100 °C , teplota varu tetrachlormetanu je asi 77 °C . Pokud bychom však tento systém zahřívali, dočkali bychom se překvapení. K varu (vzniku bublin) totiž dochází již při asi 66 °C . Vysvětlete zdánlivou podivnost.
Našel Matouš v sovětské sbírce.
E. poznej své tělo
Na závěr ročníku pro vás máme jednoduchou experimentální úlohu. Z následujících tělních tekutin si vyberte alespoň dvě a změřte jejich alespoň jednu fyzikální vlastnost (hustotu, viskozitu, elektrickou vodivost, index lomu, teplotu varu, …) – sliny, krev, moč, pot, slzy, žaludeční šťávy, míza.
V této úloze se řiďte heslem čím více, tím lépe.
Tuto hovadskou úlohu vymysleli Jarda s Honzou po ICQ těsně před tiskem.
S. poslední úloha
- Kvalitativně popište, jak se chová tepelná kapacita Isingova modelu s nulovým vnějším magnetickým polem v okolí kritické teploty.
- Podobným postupem, jako jsme vypočítali chování magnetizace $m$ v okolí kritického bodu, určete chování susceptibility $χ$ ($lim_{B→0}∂m⁄∂B$) a závislost magnetizace na magnetickém poli při kritické teplotě.
- Ukažte, že model mřížového plynu vede ke kondenzaci a určete kritickou teplotu.
- Prozkoumejte model binární slitiny.
Zadal autor seriálu Matouš Ringel.