4. Série 22. Ročníku
Termín uploadu: -
1. Kyklopovo zrcadlo
Zkuste vypočítat, jaký tvar by mělo mít zrcadlo, tak, aby se v něm kyklopova hlava jevila jako čtverec. Kyklop má hlavu ve tvaru koule s okem uprostřed.
Při pohledu do zrcadla uviděl Mára.
2. na tenkém ledě
Je známo, že led vystavený většímu tlaku snižuje svou teplotu tání. Funguje tento jev při bruslení (tedy, je tlak brusle dostatečný, aby se led rozpustil i při nízkých teplotách)? Pokud ne, co jiného zaručuje hladký skluz?
Při návštěvě kluziště si počítal Dan.
3. vlček neboli káča
Inženýři v NASA chtějí využít setrvačníků jako zdroje energie pro družice. Poraďte jim, jakou maximální energii mohou uložit do rotujícího válce o poloměru $r$. Na jakou maximální úhlovou rychlost $ω$ lze roztočit setrvačník, než praskne?
Na podobný problém narazil Robin.
4. šachovnice
Jistě znáte pohádku o chytrákovi, který si udělal legraci z krále tím, že mu dal za úkol na políčka šachovnice vyskládat postupně 1, 2, 4, 8, 16, …, 2^{63} zrníček rýže po řádcích zleva doprava). Většinou se ale nedodává, že se chytrák velmi podivil, když král šachovnicový stolek nechal přinést. Spočtěte, kde byl vypodložen, aby zrníčka nespadla. Zrníčka jsou hmotné body umístěné ve středu polí. (Přesněji řečeno nás zajímá poloha těžiště šachovnice s rýží.)
Několik vagónů rýže si objednal Jakub Michálek.
P. zachraňte fyziku
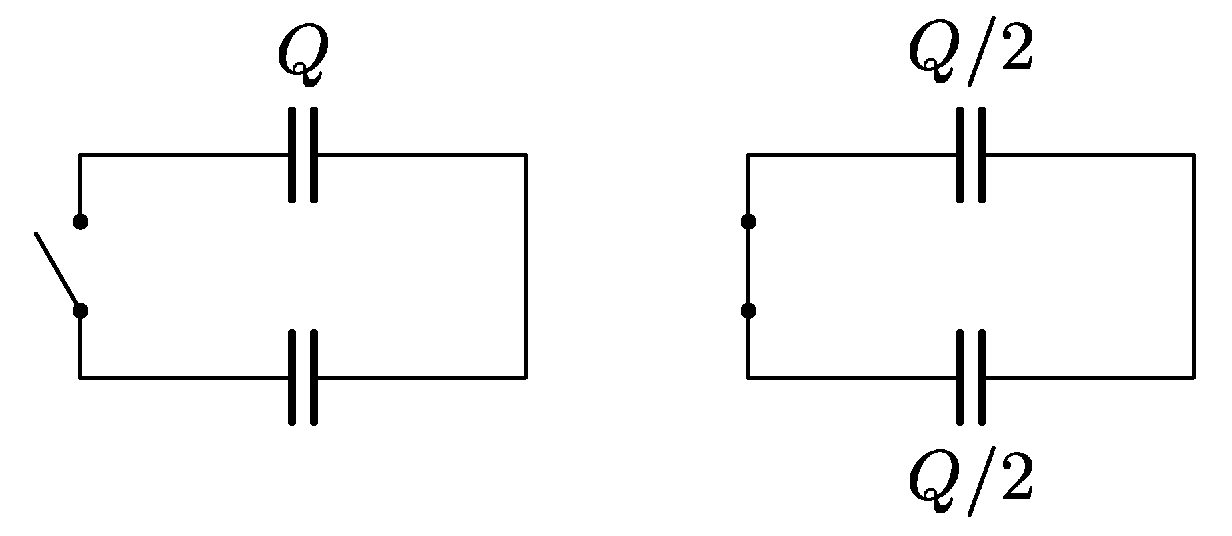
Rozpojený obvod na obrázku obsahuje jeden nenabitý a jeden nabitý kondenzátor (náboj $Q)$. Vodiče jsou ideální, nemají žádný odpor, oba kondenzátory jsou stejné. Celková energie nábojů v obvodu tedy je $Q⁄2C$. Pokud se po sepnutí vypínače náboje na kondenzátorech vyrovnají, celková energie bude $Q⁄8C+Q⁄8C=Q⁄4C$, což je polovina oproti počáteční situaci. Vysvětlete tento rozdíl. Kde se spotřebovala polovina energie? Vypínač je vyrobený tak šikovně, že v něm vysvětlení netkví.
S touhle záludností přišel Jarda Trnka.
E. blowjob
Kupte si nafukovací balonek, nafoukněte jej, zavažte a proměřte, jak se jeho objem mění s časem. Pokuste se určit, kolik z plochy balonku zabírají póry, kterými vzduch uniká.
Před jarním soustředěním se zamyslel Aleš.
S. Foucaultovo kyvadlo a rotace Země
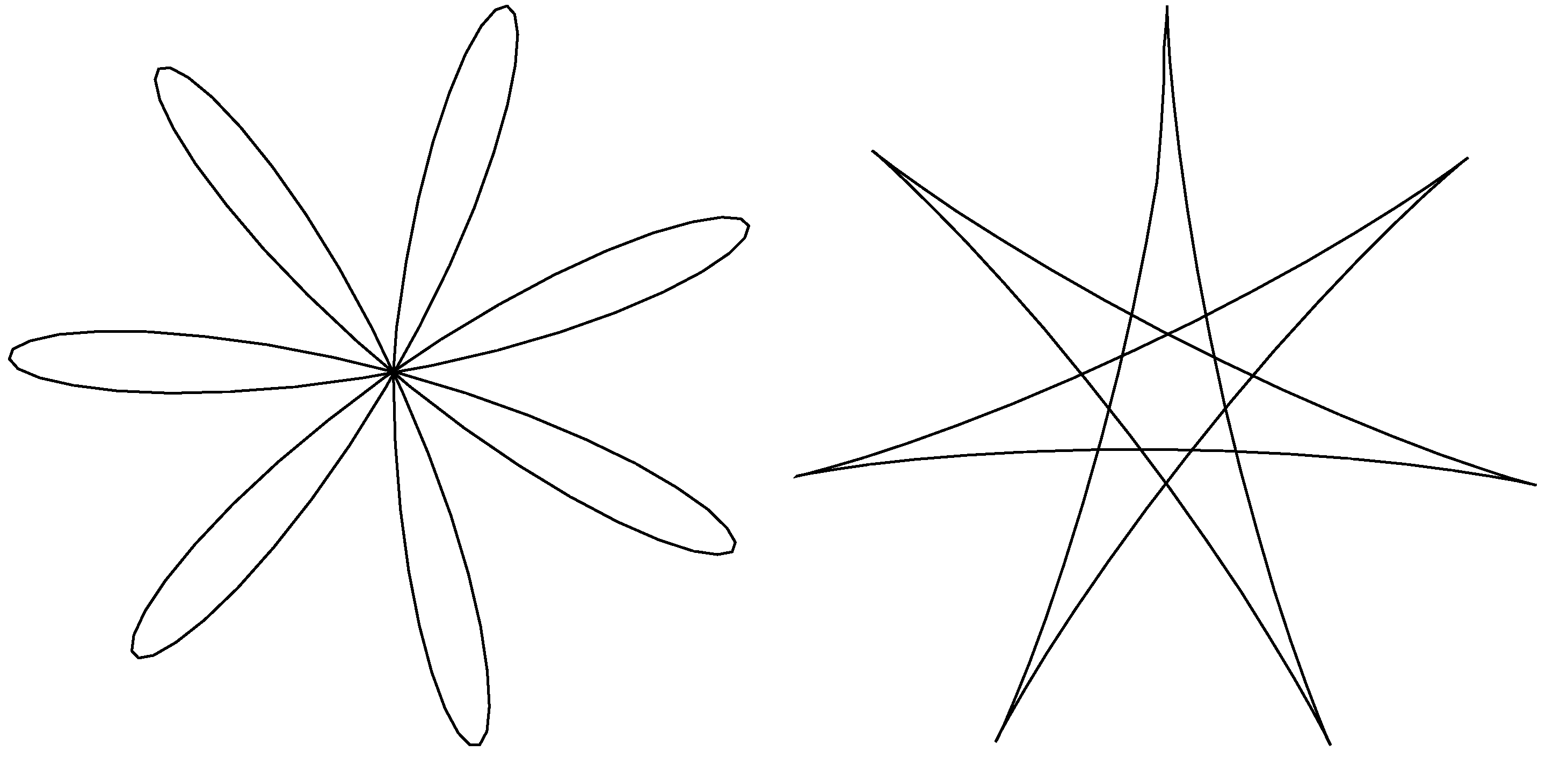
- Foucaultovo kyvadlo do písku nakreslilo při dvou různých demonstracích dva odlišné obrazce, oba jsou na obrázku. Rozhodněte, co způsobilo jiný tvar a také jak dlouhé by muselo být kyvadlo, aby tyto obrazce mohly na podlaze pařížské katedrály vzniknout. Kolikacípé jsou hvězdy/květy ve skutečnosti?
- Jaký tvar bude mít hladina v kbelíku s vodou, který klidně stojí na rovném stole?
- Ukažte, že vztah
$$δf=f_{+}-f_{-}=\frac{4ωS}{λ_{0} P}$$ pro frekvenční rozdíl (frekvenci rázů) dvou protiběžných paprsků v laserovém gyroskopu platí pro jeho libovolný rovinný tvar – tedy nejen kruhový.
K procvičení probrané látky zadali autoři seriálu.