5. Série 23. Ročníku
Termín uploadu: -
1. fotonová fontána
Honza není spokojen se současným standardem postelí, a proto začal testovat levitaci na laseru. Koupil si kuličku s dokonale vyleštěným zrcadlovým povrchem o hmotnosti $m$, poloměru $r$ a položil ji na zem. Podlaha se rozzářila lasery o vlnové délce $λ$ a plošném výkonu $P$. V jaké výšce nad zemí se kulička ustálila? Za bonusové body můžete vyřešit situaci, kdy je kulička skleněná. V obou případech uvažujeme, že ji laser neroztaví a že se experiment odehrává v homogenním gravitačním poli.
Do fyziklání přinesl Honza Humplík
2. Lukášovo péro
Ve starém gauči našel Lukáš pružinu o tuhosti $k$, poloměru závitu $r$, délky $l$ a počtem závitů $n$. Protože se nudil, připojil ji ke stabilnímu zdroji elektrického proudu $I$. Jak se změnila její tuhost?
vymyslel Lukáš, když mu Aleš řekl, aby něco vymyslel
3. vozík
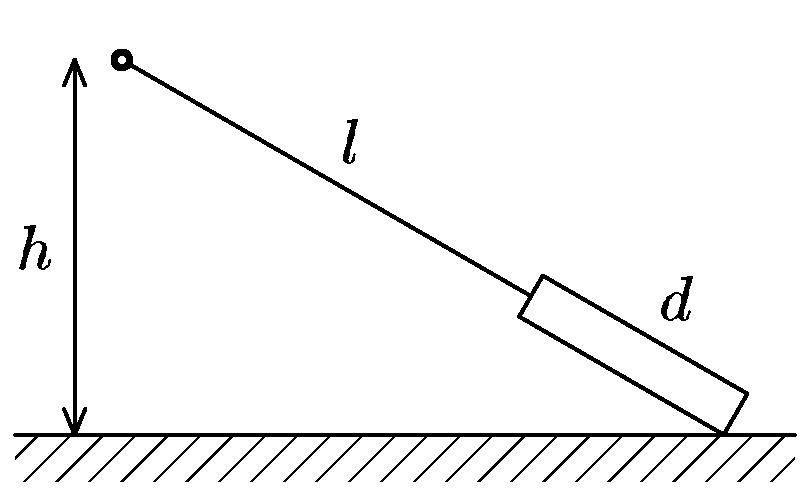
Na pevném závěsu ve výšce $h=1\, \mathrm{m}$ nad zemí je upevněn provázek délky $l=1,5 \;\mathrm{m}$. Na konci provázku je přivázána deska délky $d= 0,5 \;\mathrm{m}$ tak, že provázek je napnut a spolu s deskou leží v jedné přímce (viz obrázek). Když soustavu uvolníme, deska nejprve po hraně klouže bez tření, dokud nedopadne celou svou délkou na zem. Potom se pohybuje proti třecí síle s koeficientem smykového tření $f$. Spočítejte, jaká musí být jeho hodnota, aby deska svým bližším koncem doklouzala přesně pod závěs.
jako triviální úlohu do fyziklání vymyslel Lukáš
4. drtivý odpad
Všichni dobře víme, že se 21. prosince 2012 na své cestě ke Slunci srazí se Zemí asteroid (pohybuje se ve stejné rovině jako Země). Uvažme, že se pohybuje po protáhlé eliptické dráze s hlavní poloosou délky 4 AU a vedlejší poloosou dlouhou 0,2 AU. Lidstvo bylo moc zaneprázdněno, a tak se problém začal řešit až 1. prosince 2012. Po jaké dráze musí udatná světová autorita vystřelit raketu s jadernou hlavicí, aby včas odvrátila konec světa?
napadlo Honzu Humplíka
P. tunelářská
Kryštof se vydal na cestu vlakem a spokojeně usnul. Když se probudil v tunelu, cítil, že jej nějaká síla táhne směrem na jednu stranu. Ve vlaku bylo sice světlo, ale ven neviděl. Vzpomněl si, že je v zatáčkách trať klopená a uvědomil si, že i když si pamatuje původní směr jízdy, vůbec neví, na kterou stranu vlak zatáčí. Nepozná totiž rozdíl mezi stavem, kdy vlevo zatáčející vlak jede dostatečně pomalu a výsledná síla míří směrem do zatáčky, a situací, kdy je vlak dostatečně rychlý, zatáčí vpravo a síla směřuje ven ze zatáčky. Navrhněte experiment, který Kryštofovi pomůže tuto situaci vyřešit. Čím víc variant, tím lepší bodové hodnocení.
cestou metrem napadlo Kryštofa
E. ozvěna
Když stojíte v malém prostoru a zahrajete správný tón, můžete objevit jeho rezonanční frekvenci. Protože rezonanční frekvence přímo souvisí s rozměry rezonátoru, umíme je z její znalosti určit. Vyhlédněte si doma vhodnou místnost (ideální jsou malé rozměry a holé stěny; třeba toaleta), tímto způsobem ji změřte a porovnejte výsledky se skutečností.
na záchodě si notoval Jakub Michálek
S. světlo v látce
- Index lomu v nelineárním materiálu závisí na intenzitě světla $I$ jako $n=n_{1}+n_{2}I$, kde $n_{1}$ a $n_{2}$ jsou konstanty větší než nula. Zamyslete se, co se bude dít s paprskem světla dané šířky, který tímto materiálem prochází. Předpokládejte, že intenzita paprsku klesá se vzdáleností od jeho středu. (Stačí kvalitativní úvaha, odvážnější se mohou pokusit vybudovat analytický model.)
- Deska tloušťky $a$ sestává z 2$N$ stejně širokých rovnoběných destiček ze dvou materiálů o indexech lomu $n_{1}$ a $n_{2}$ poskládaných na střídačku. Světelná vlna dopadá kolmo na čelní destičku. Jaký bude efektivní index lomu této smíchané desky pro $N→∞?$ Napadá vás proč? ( Nápověda: pro libovolnou matici $A$ platí $\rm{lim}_{N→∞}(I+A⁄N)^{N}=\exp(A)$, kde $I$ je jednotková matice a exp$(A)=I+A+A⁄2!+A⁄3!+\ldots)$
Po dlouhém boji vyplodili hoši z Cambridge.