5. Série 27. Ročníku
Termín uploadu: -
(2 body)1. natlakovaná žirafa
Porovnejte krevní tlak v hlavě dospělé žirafy a dospělého člověka. Systolický tlak na úrovni srdce je u člověka $p_{h1}=120\;\mathrm{mm}Hg$ a u žirafy $p_{g1}=280\;\mathrm{mm}Hg$, hustota krve obou živočichů je $ρ=1050\;\mathrm{kg\cdot m^{-3}}$. Uvažujte pouze případ, kdy člověk i žirafa stojí. Rychlost proudění krve v těle považujte za konstantní.
Mirek přemýšlel, proč žirafa neomdlí.
(2 body)2. uranová hvězda
Představme si, že ve hvězdách neprobíhá termojaderná fúze, nýbrž štěpná jaderná reakce. Odhadněte, jak dlouho by taková hvězda dokázala vyzařovat, jestliže na počátku svého životního cyklu sestává pouze z uranu 235, její hmotnost i zářivý výkon jsou přibližně konstantní a odpovídají současným hodnotám pro Slunce.
Mirek si pročítal nové učebnice.
(3 body)3. ta jemná nádoba
Mějme válcovou nádobu, jež zaujímá objem $V=1\, \jd{l}$. Nádoba je uzavřena vzduchotěsným pohyblivým pístem, který má nezanedbatelnou hmotnost $M$. Dále víme, že nádoba je vodorovnými přepážkami rozdělena na $n$ komor a v $i$-té komoře (číslováno odshora) je $2^{i}a$ částic, kde $a$ je blíže neurčená konstanta. Přepážky nejsou k nádobě připevněny, přesto nedovolují, aby si komory, v nichž je ideální plyn, vyměňovaly teplo nebo částice. Celý systém je v rovnováze. Poté zdvojnásobíme hmotnost pístu a počkáme, až se náš systém opět ustaví v rovnováze. Jak se změní objem, který plyn v nádobě zaujímá? Atmosferický tlak neuvažujte.
Náry pod tlakem vymyslel úlohu o tlaku.
(4 body)4. trojúhelníkový odporníček
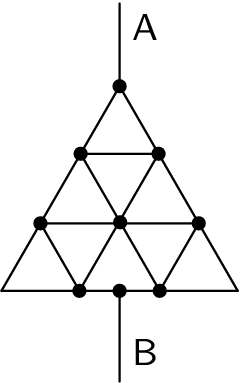
Určete odpor trojúhelníku vytvořeného z odporového drátu mezi svorkami A a B, které vidíte na obrázku. Jedna strana malého trojúhelníčku (ze kterých se skládá velký trojúhelník) má odpor $R_{0}$. Odpor přívodních vodičů neuvažujte.
Karel si maloval trojúhelníčky.
(5 bodů)5. hlídání dětí
Mějme houpačku zavěšenou na dvou svislých lanech délky $l=1,5\;\mathrm{m}$ na vodorovné tyči o poloměru $r=4\;\mathrm{cm}$. Dítěti sedícímu na houpačce udělíme v dolní úvrati takovou rychlost $v_{0}$, aby dítě vykonalo celou otočku kolem horizontální tyče a lana byla během namotávání stále napnutá. Zároveň chceme, aby počáteční rychlost byla nejmenší možná. Určete rozdíl úhlové rychlosti $ω_{1}$ houpačky s dítětem po návratu do dolní úvrati a počáteční úhlové rychlosti $ω_{0}$.
Nápověda: Pro výpočet odstředivého zrychlení můžete uvažovat, že se dítě pohybuje lokálně po kružnici.
Mirek si vždycky rád hrál s mladšími sourozenci.
(5 bodů)P. fyzika v plamenech
Na jakých fyzikálních (a chemických) parametrech závisí teplota, kterou hoří nějaká konkrétní látka? Jak? Určete tuto teplotu pro nějakou konkrétní látku.
Karel přemýšlel nad plamenem
(8 bodů)E. gumipuk
Závaží o hmotnosti $m$ na gumičce délky $l_{0}$ je zavěšeno v pevném bodě o souřadnicích $x=0$ a $y=0$. Z osy $x$, která je horizontálně, závaží pouštíme. Jaká bude závislost nejnižšího dosaženého bodu na poloze na ose $x?$
Dominika zkoušela, jak co nejlépe někomu vypíchnout oko.
(6 bodů)S. struna
Uvažujme otevřené struny a omezme se jen na tři prostorové rozměry. Namalujte, jak vypadá
- struna volně se pohybující v časoprostoru,
- struna připevněná oběma konci k D2-bráně,
- struna natažená mezi D2-bránou a D1-bránou.
Jaké jsou možnosti, kde mohou struny končit v případě konfigurace tří rovnoběžných D2-brán?
Vyberte si jednu z funkcí $\mathcal{P}_{\mu}^{\tau}$ nebo $\mathcal{P}_{\mu}^{\sigma}$ definovanou v první části seriálu a najděte její explicitní tvar (tj. přímo závislost na $\dot{X}^{\mu}$ a $X'^{\mu}$). Ukažte, že podmínky $\vect{X}'\cdot \dot{\vect{X}}=0$ a $|\dot{\vect{X}}|^2=-|\vect{X}'|^2$ opravdu vedou na zjednodušení uvedené v textu.
Najděte spektrum energií harmonického oscilátoru.
- Energie harmonického oscilátoru je dána Hamiltoniánem
$$\hat{H}=\frac{\hat{p}^2}{2m} + \frac{1}{2}m\omega^2\hat{x}^2\,.$$ Druhý člen je očividně potenciální energií zatímco první dává po dosazení $\hat{p}=m\hat{v}$ kinetickou energii. Definujme lineární kombinaci $\hat{\alpha}=a\hat{x} + \;\mathrm{i} b\hat{p}$. Určete reálné konstanty $a$ a $b$, tak aby měl Hamiltonián tvar $$\hat{H}=\hbar \omega \left(\hat{\alpha} ^{\dagger}\hat{\alpha} + \frac{1}{2}\right)\,,$$ kde $\hat{\alpha} ^{\dagger}$ je komplexní sdružení $\hat{\alpha}$.
- Ukažte ze znalosti kanonických komutačních relací pro $\hat{x}$ a $\hat{p}$, že platí
$$\left[\hat{\alpha},\hat{\alpha}\right]=0\,,\quad\left[\hat{\alpha} ^{\dagger},\hat{\alpha} ^{\dagger}\right]=0\,,\quad\left[\hat{\alpha} ,\hat{\alpha} ^{\dagger}\right]=1$$
- Ve spektru oscilátoru bude určitě stav s minimální energií odpovídající nejmenšímu možnému kmitání. Označme ho $|0\rangle$. Tento stav musí splňovat $\alpha |0\rangle =0$. Ukažte, že je jeho energie rovna $\hbar\omega/2$, tj. $\hat{H}|0\rangle=\hbar\omega/2|0\rangle$. Dále ověřte, že pokud by bylo $\alpha |0\rangle \neq 0$, pak máme spor s tím, že má $|0\rangle$ minimální energii, tj. $\hat{H}\alpha |0\rangle=E\alpha|0\rangle$, kde nyní je $E<\hbar\omega/2$. Všechny vlastní stavy Hamiltoniánu můžeme potom psát jako $\left(\alpha^{\dagger}\right) ^n|0\rangle$ pro $n=0,1,2,\dots$ Najděte energie těchto stavů, tj. čísla $E_n$ taková, že $\hat{H}\left(\alpha^{\dagger}\right) ^n|0\rangle=E_n\left(\alpha^{\dagger}\right)^n|0\rangle$
Tip Použijte komutační relace pro $\hat{\alpha}^{\dagger}$ a $\hat{\alpha}$ .