4. Série 2. Ročníku
Termín uploadu: -
1. vozík
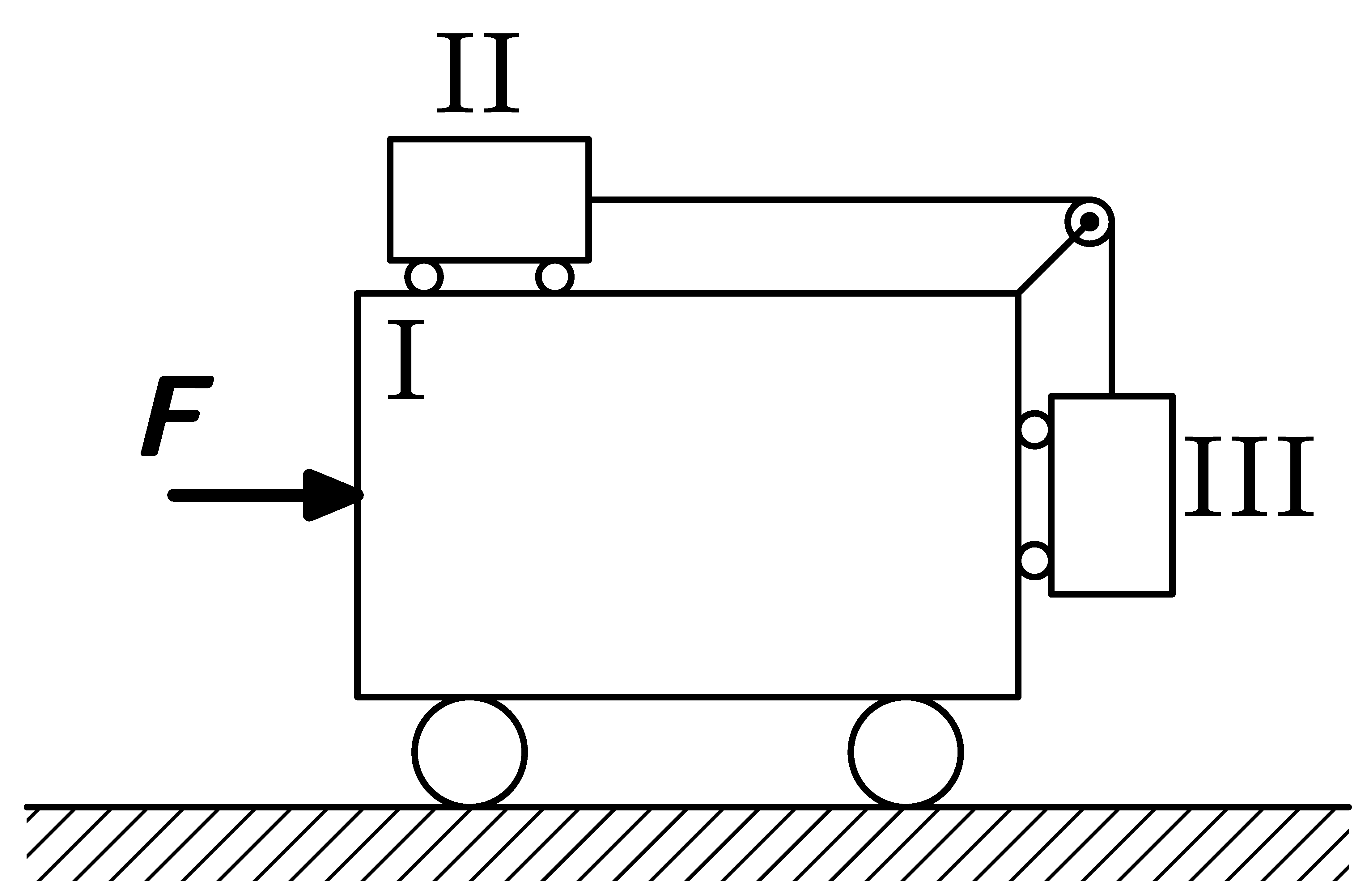
Model tří těles
Mějme soustavu vyobrazenou na obrázku. Jakou silou $\textbf{F}$ musíme působit, aby se těleso II nepohybovalo vůči tělesu I. Máte zadané hmotnosti $m_{I}$, $m_{II}$ a $m_{III}$ všech tří těles a veškerá tření zanedbávejte.
2. mouchy
Postavme na váhu uzavřenou sklenici s několika muškami. Kdy nám váha ukazuje více, když mušky ve sklenici
- létají
- usedly
- v obou případech váha ukazuje stejně
Proč?
3. reflektor
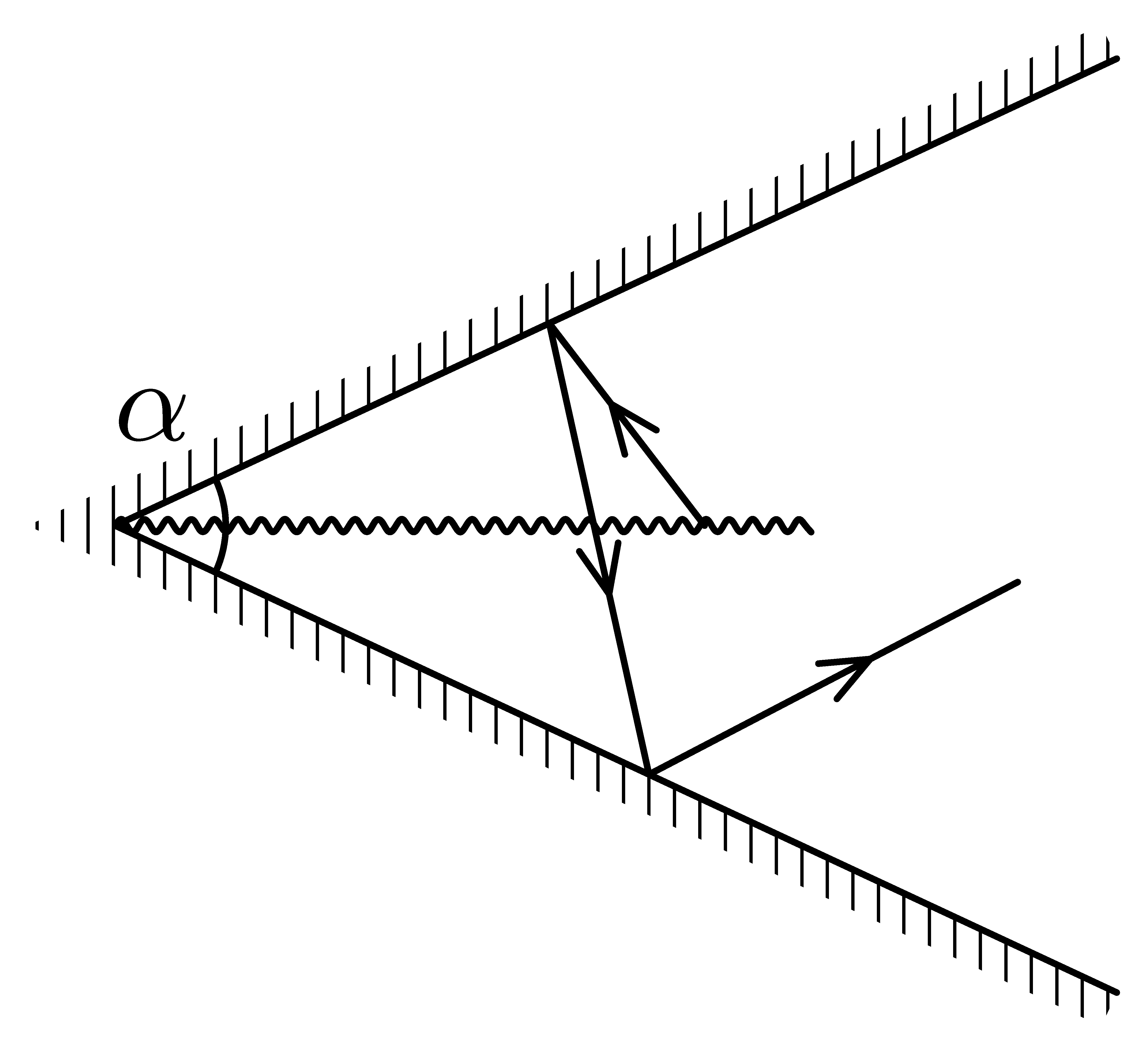
Reflektor
Jaký musí být vrcholový úhel kuželového reflektoru, aby se paprsky ze svítícího vlákna v ose kuželu délky $l$ odrazily o stínítko jednou, dvakrát, $n$-krát? Stínítko je dostatečně velké.
4. kondenzátor
Kondenzátor z dvou desek plochy $S$ vzdálených $l_{1}$ nabijeme baterií o napětí $U_{B}$. Jaku práci musíme vykonat k oddálení desek na vzdálenost $l_{2}$, když jsme přetím baterii
- odpojili
- neodpojili
Jestliže se práce v případě a) a b) liší, vysvětlete, jaké „tajemné síly“ tento rozdíl způsobují. Rozměry desek jsou mnohem větší než vzdálenosti $l_{1}$ a $l_{2}$.
E. magnetizmus
Jistě jste se již setkali s magnetickými jevy – např. přitahováním a odpuzování magnetů, schopností magnetu působit na železné předměty apod. Někteří z vás vědí, že magnetické účinky má i elektrický proud (a že tyto jevy jsou fyzikálně snáze vysvětlitelné než účinky permanentních magnetů). Teoretické rozbory nechme ale zatím stranou. Zkuste experimentálně zjistit magnetické vlastnosti různých, i vámi vyrobených cívek, jejich vzájemné silové působení v závislosti na počtu závitů, proudu, orientaci, kvalitě jádra (tj. materiálu, na kterém je cívka namotaná), resp. čáry magnetické indukce v okolí cívky a různé další vlastnosti, které vás napadnou.
S. polární souřadnice
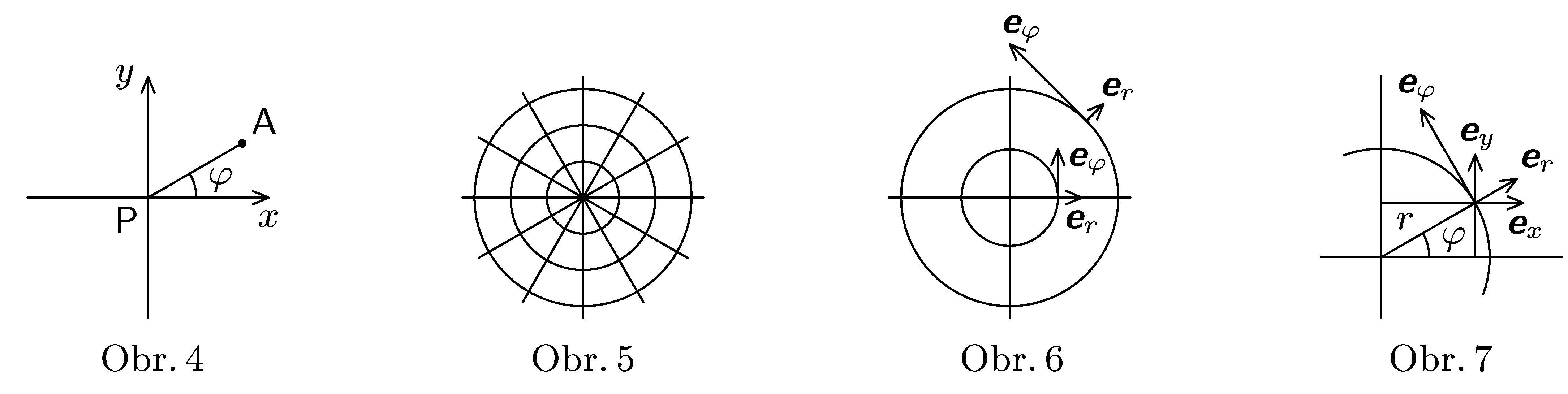
Polární souřadnice
- Polární souřadnice bodu A v rovině je dvojice čísel $r$, $φ$, udávající vzdálenost bodu $A$ od počátku a úhel polopřímky $PA$ a osy $x$ (obr. 4). Odvoďte transformační vztahy od polárních souřadnic $r$, $φ$ ke kartézským souřadnicím $x$, $y$.
- U polárních souřadnic hraje roli souřadných os přímky procházející počátkem a kružnice se středem v počátku (obr. 5) - na těchto křivkách je vždy jedna souřadnice konstantní. Vektory báze se nyní volí v každém bodě tečné k souřadnicovým osám v tomto bodě a délky $|\textbf{e}_{r}|=1$, $|\textbf{e}_{φ}|=r$ (obr. 6). V tomto případě nejsou již vektory báze v různých bodech rovnoběžné, jak tomu bylo v případě kartézských souřadnic. Odvoďte transformační vztahy od souřadnic $b_{r}$, $b_{φ}$ k $b_{x}$, $b_{y}$ vektoru $\textbf{b}$ vedoucího z bodu $A$. Souřadnice $b_{r}$, $b_{φ}$ jsou počítané vůči bázi $\textbf{e}_{r}$, $\textbf{e}_{φ}$ v bodě $A$ (polární souřadnice), $b_{x}$, $b_{y}$ jsou počítané vůči bázi $\textbf{e}_{x}$, $\textbf{e}_{y}$ (kartézské souřadnice) a bod $A$ má polární souřadnice $r$, $φ$ (viz obr. 7).