6. Série 22. Ročníku
Termín uploadu: -
1. odpor je marný
Vypočítejte odpor $n$-rozměrné krychle mezi dvěma nejvzdálenějšími vrcholy (ty o souřadnicích $(0$, $0$, …, $0)$ a $(1$, $1$, …, $1)$. Zkuste začít od trojrozměrné a použijte stejný postup.
Přednesl Lukáš Ledvina
2. útěk z koule
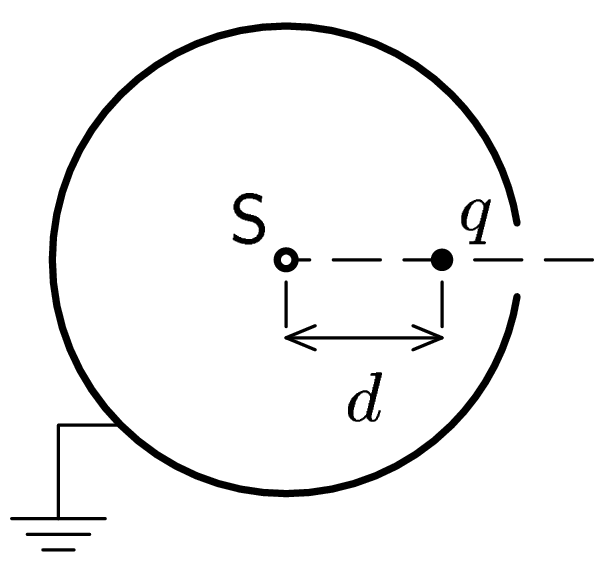
V uzemněné kouli z vodivého materiálu je vyvrtán malý otvor, tak akorát, že ním projde malá nabitá částice. Umístíme ji do vzdálenosti $d$ od středu koule na spojnici jejího středu a otvoru (viz obrázek). Náboj pustíme. Jak daleko z koule vyletí ven? Zkuste využít metodu zrcadlového potenciálu.
nad koulemi rozjímal Pavel M.
3. relativistická koule
Při pohybu rychlostí srovnatelnou s rychlostí světla dochází ke kontrakci délek, ale zároveň se nám předmět zdá delší než ve skutečnosti je (zkuste sledovat paprsky světla vyslané z bližšího a vzdálenějšího konce tělesa). Vypočítejte, jestli se u relativistické koule tyto efekty nevyruší.
z Cambridge donesl Dalimil
4. kámen na pístu
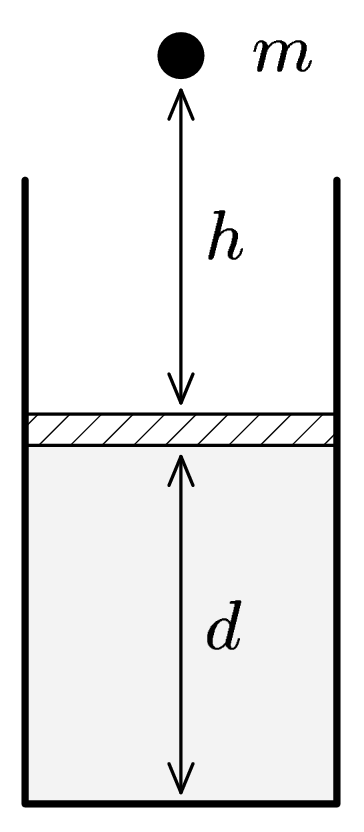
Marek má píst o rozměru $S$ s ideálním plynem v rovnovážném stavu ($p$, $V$ a $T)$. Na tento píst z výšky $h$ pustí kámen o hmotnosti $m$ (viz obrázek). Píst se stlačí a opět vrátí do nějaké polohy zpět. Jak závisí tato poloha na hmotnosti kamene a výšky, ze které byl upuštěn? Je možné, že se píst ustálí ve vyšší poloze než byl prve? Jak se změní teplota plynu v pístu?
vymyslel Mára po přednášce z termodynamiky
P. lidští ptáci
Titan – družice Saturnu – je mrazivý svět (povrchová teplota asi $94\, \jd{K}$) s mohutnou dusíkovou atmosférou, s ledovým povrchem a uhlovodíkovými jezery. Průměr Titanu je $5\,150\, \jd{km}$, hmotnost je $1/45$ hmotnosti Země, tloušťka jeho atmosféry je $200\, \jd{km}$ a tlak na jeho povrchu je $1,\!5$ atmosféry.
Na základě předložených údajů určete gravitační zrychlení na povrchu a odhadněte hustotu atmosféry. Srovnáním s parametry ptáků v pozemských podmínkách rozhodněte, zda by opeřený člověk mohl na Titanu létat.
Létat se zachtělo Honzovi P.
E. vratné lahve
Kupte si standardní skleněnou lahev od piva nebo minerálky a změřte, jak závisí výška tónu vydaného po fouknutí na hrdlo na výšce vodní hladiny v lahvi.
vymysleli organizátoři na pravidelné schůzi
S. atomové modely a Rutherfordův experiment
- Rozhodněte, zda stabilita (popř. rozměr) saturnského atomového modelu závisí na atomovém čísle $Z$.
- Upravte vzorec (12) pro pravděpodobnost rozptylu $α$-částice pod velkým úhlem $φ$ tak, abyste dostali praktičtější vztah pro pravděpodobnost dopadu na jednotku plochy scintilátoru, a uvažte, jak byste ho využili k určení materiálu ostřelovaného vzorku. Dále odhadněte, jak by se vzorec změnil, pokud bychom neuvažovali centrální náboj $Ze$ nýbrž $Z$ rozptýlených elementárních nábojů $e$ jako třeba v Lenardově modelu.
- V roce 1896 objevil astronom E. C. Pickering ve světle hvězdy $ζ$ Puppis čáry, které splňovaly vztah (7) pro $n=2$ a $m=2,\!5$; $3$; $3,\!5$; $4$; $4,\!5$; …, tedy i pro polocelá čísla! Vysvětlete tuto zdánlivou nesrovnalost s Bohrovým modelem.
- Bonus: Najděte závislost analogickou rovnici (11) pro Thompsonův pudinkový model a okomentujte rozdíly. Nebo zkuste (11) upravit tak, aby zahrnovala působení jader všech atomů v tenké fólii. Zkrátka si trochu vyhrajte.
Na rozloučenou od autorů seriálu.