2. Série 2. Ročníku
Termín uploadu: -
1. loď ve vaně
Může bitevní loď plavat ve vaně? Máme samozřejmě na mysli dostatečně velkou vanu nebo dostatečně malou loď. V každém případě je okolo lodě celkem málo vody. Mějme konkrétně loď s hmotností $100\; \textrm{tun}$ a vanu, ve které je $1\; \textrm{m}$ vody.
2. dvě kuličky
Uvažujme tělísko o hmotnosti $m$ nacházející se v klidu v gravitačním poli velmi těžké kuličky, jejíž velikost lze zanedbat, s hmotností $M\gg m$. Zkuste spočítat nebo odhadnout dobu, za kterou tělísko dopadne na kuličku, je-li mezi nimi na začátku vzdálenost $R$. Zkuste navrhnout fyzikální situaci odpovídající této sestavě.
3. jak rychlá je lokomotiva?
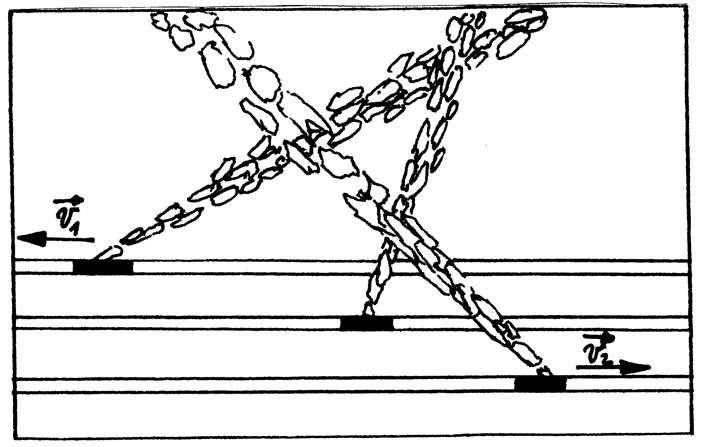
Snímek lokomotiv
Na obrázku je letecký snímek parních lokomotiv s oblaky páry pohybujících se rovnoměrně po přímých rovnoběžných kolejích. Rychlost první lokomotivy je $v_{1}=50\;\mathrm{km}\cdot \textrm{h}^{-1}$, rychlost druhé $v_{2}=70\;\mathrm{km}\cdot \textrm{h}^{-1}$. Směry rychlostí jsou vyznačeny na obrázku. Jaká je rychlost třetí lokomotivy?
4. výška sloupce vzduchu
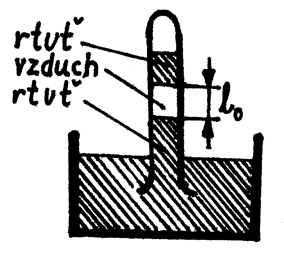
Barometrická stupnice
V barometrické trubici je sloupec vzduchu. Při teplotě $t_{0}=10^{\circ}\;\mathrm{C}$ je výška sloupce $l_{0}=10\;\mathrm{cm}$. Jaká bude jeho výška při teplotě $t=30^{\circ}\;\mathrm{C}$?
E. homole
Sypeme-li přášek (suchý písek, mouku apod.) volně na jedno místo, vznikne kužel s vrcholovým úhlem $α$. Co lze o tomto úhlu pokusně zjistit? Umíte výsledek nějak zdůvodnit?
S. vektory
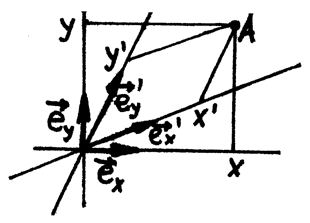
Dvě soustavy
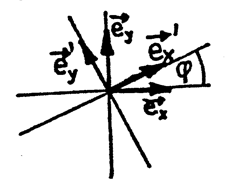
Obecné soustavy
- Mějme zadané dvě soustavy souřadnic pomocí vektorů $\textbf{e}_{x}$, $\textbf{e}_{y}$ a $\textbf{e}_{x}′$, $\textbf{e}_{y}′$ a společného počátku $P$. Vzájemnou polohu soustav máme zadanou pomocí souřadnic $a_{xx}$, $a_{xy}$, $a_{yx}$, $a_{yy}$ vektorů $\textbf{e}_{x}′$, $\textbf{e}_{y}′$ vůči bázi $\textbf{e}_{x}$, $\textbf{e}_{y}$. $\textbf{e}_{x}′=a_{xx} \textbf{e}_{x}+a_{xy} \textbf{e}_{y}$, $\textbf{e}_{y}′=a_{yx}\textbf{e}_{x}+a_{yy}\textbf{e}_{y}$. Odvoďte transformační vztahy mezi souřadnicemi $x$, $y$ a $x′$, $y′$ v závislosti na koeficientech $a_{xx}$, $a_{xy}$, $a_{yx}$, $a_{yy}$ (tj. předpis, jak z $x$ a $y$ vypočítat $x′$ a $y′$ a naopak).
- Jelikož obě soustavy mohly být obecné (nepravoúhlé, bez stejných jednotek), bylo potřeba k zadání vzájemného vztahu soustav udat čtyři koeficienty $a_{xx}$, $a_{xy}$, $a_{yx}$, $a_{yy}$. Pokud budou obě soustavy kartézské (pravoúhlé s jednotkovým měřítkem), tak musí být délky vektorů $\textbf{e}_{x}$, $\textbf{e}_{y}$ resp. $\textbf{e}_{x}′$, $\textbf{e}_{y}′$ jednotkové a vektory musí být na sebe kolmé. K udání vzájemné polohy pak stačí zadat vzájemný úhel $φ$. Jak souvisí v tomto případě koeficienty $a_{xx}$, $a_{xy}$, $a_{yx}$, $a_{yy}$ s úhlem $φ$?