4. Série 7. Ročníku
Termín uploadu: -
1. vláček
Dlouhá vlaková souprava délky $l$ jede po dráze, která z vodorovného úseku přechází ve svah se sklonem $a$. V okamžiku, kdy se vlak zastavil, byla na svahu přesně polovina vagónů. Jaká byla doba, za kterou vyjely tyto vagóny na svah. Tření zanedbejte.
2. kužel
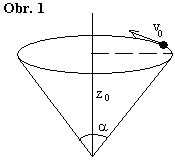
Hmotný bod se v tíhovém poli Země pohybuje po vnitřku kuželové plochy s vrcholovým úhlem $2α$, jejíž osa symetrie má svislý směr (viz obr. 1). V čase $t=0$ se částice nachází ve výšce $z_{0}$ a má rychlost $v_{0}$. Tato rychlost má směr tečny ke kružnici na průniku kužele s vodorovnou rovinou $z=z_{0}$.
- Obíhá-li částice v konstantní výšce $z_{0}$, dokažte, že velikost rychlosti je určena pouze touto výškou a nezávisí na úhlu $α$.
- Při obecném pohybu určete body obratu $z_{1}$ a $z_{2}$, tj. maximální a minimální výšku, do které částice vystoupí.
Diskutujte trajektorii částice v soustavě spojené s částicí a soustavě spojené se Zemí. Tření neuvažujte.
3. nešikovný cyklista
Roztržitý cyklista nezpozoroval, že v plné rychlosti najel do betonové zídky stojící kolmo k jeho dráze. Jakou nejvyšší rychlostí mohl jet, když nedošlo k deformaci ráfku.
P. čočka
Čočka je věc natolik známá, že si asi každý myslí, že zde již žádné problémy nejsou. Opak je pravdou. Čočky mají spoustu vad a jedna z nich je způsobena závislostí indexu lomu na vlnové délce. V praxi se vyrábějí takové čočky, aby pokud možno lámaly světlo všech vlnových délek stejně. Takové čočky se vyrábějí z více materiálů a požadavkem je, aby několik zadaných vlnových délek prošlo stejně. Vaším úkolem bude navrhnout takovou plosku-vypouklou čočku (plochá je u 1. materiálu).
- Máte 2 materiály o indexu lomu $n$ a dvě zadané vlnové délky $λ_{1}$ ,$λ_{1}$:
| 1. materiál | 2. materiál | |
| $λ_{1}$ | $n_{1,1}$ | $n_{1,2}$ |
| $λ_{2}$ | $n_{2,1}$ | $n_{2,2}$ |
Z těchto materiálů navrhněte plosko-vypouklou čočku (tj. najděte vhodné poloměry křivosti ploch při daném pořadí materiálů) o optické mohutnosti $D$. Čočka bude ve vzduchu, tj. $n=1$.
- Jelikož lidské oko je citlivé hlavně na tři barvy (červená, zelená a modrá), je velmi důležitá tato úloha: Máte 3 materiály s indexy lomu
| barva | tavený křemen | Schott K3 | Eastman Kodak – 110 |
| červená | $1,454$ | $1,512$ | $1,689$ |
| zelená | $1,459$ | $1,518$ | $1,697$ |
| modrá | $1,470$ | $1,533$ | $1,718$ |
Nalezněte příslušné poloměry křivosti $r_{1}$, $r_{2}$, $r_{3}$. (Pořadí materiálů je 1., 2., 3. a čočka je plochá u 1.).
- Pokuste se napsat obecný postup řešení (rovnici a algoritmus řešení) tohoto problému pro $x$ vlnových délek pomocí matic. (Tento postup je např. velmi vhodný u b).)
E. moment setrvačnosti smetáku
V této experimentální úloze je našim záměrem, abyste si všichni své navržené postupy také prakticky vyzkoušeli. Vymyslete a proveďte co nepřesnější metodu měření momentu setrvačnosti kuchyňského smetáku (s dlouhou násadou a příčkou na konci) vzhledem k ose rovnoběžné s násadou i ke kolmé na ni (procházející těžištěm). Pokuste se odhadnout přesnost vašeho měření.
S. zase paradoxy
- Po objasnění problému rytířů pro vás nebude obtížné vysvětlit následující paradox. Tyč délky $d$, která se pohybuje vysokou rychlostí (ve směru své délky) vodorovně těsně nad zemí, prolétá nad ústím kanálu, jehož klidová délka je taktéž $d$. V klidu by tyč do kanálu přesně zapadla, za pohybu se ale situace komplikuje. Z hlediska kanálu (klidová soustava) se tyč zkracuje, takže by měla hladce propadnout (tyč letí tak nízko, že nemůže kanál jednoduše přeletět a přitom jsou všechny její body stále ve stejné výšce), naopak pro tyč se zkrátil kanál a tedy nepřichází v úvahu, že by se do něj vešla. Jak to tedy dopadne?
- Opusťme již pozorování jen v jednom směru a podívejte se kolem sebe. Přeneste se do automobilu jedoucího značnou (tedy relativistickou) rychlostí dlouhou ulicí. Uvážíte-li relativistické efekty a konečnou rychlost šíření světla, jak se změní podoba ulice, okolních domů i silnice v dálce?