3. Série 11. Ročníku
Termín uploadu: -
1. jeřáb
Jeřáb může zdvihat břemeno pouze konstantní svislou silou $F$. Budeme jím zvedat ze země nekonečné lano o délkové hustotě $µ$. Jakou maximální rychlost jeho horní konec během pohybu dosáhne? Jakou maximální výšku dosáhne?
2. autobus
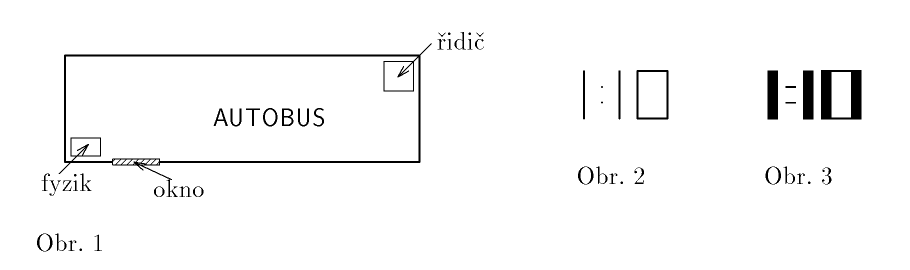
Při cestě autobusem se vám může přihodit následující podivná věc: Sedíte na zadním sedadle vpravo a díváte se z okna (viz obr. 1). Jelikož je noc, vidíte v něm také odraz digitálních hodin visících nad řidičem. Jede-li autobus pěkně po rovině, mají číslice odražené v okně zanedbatelnou tloušťku (viz obr. 2). Může se ale stát, že vlivem nerovností na vozovce a klepání motoru se okno rozkmitá a číslice se rozmažou tak, že vypadají $1 \,\jd{cm}$ tlusté (viz. obr. 3). S jak velkou amplitudou okno kmitá? Jaká musí být minimální frekvence, abychom neviděli jednotlivé kmity číslic?
3. káva a mléko
Představte si, že jste zaspali a spěcháte. Uvaříte si kávu a máte 2 minuty na to, abyste ji vypili. Káva je horká a vy potřebujete během zmíněných 2 minut dosáhnout co nejnižší teploty. Kávu pijete samozřejmě s mlékem. Na vás je, abyste rozhodli, dosáhnete-li nižší teploty, když necháte kávu 2 minuty chladnout, pak do ní nalejete mléko a nebo mléko nalejete co nejdříve? Nebo je výhodnější nalét mléko někdy v průběhu chladnutí? Mléko má samozřejmě pokojovou teplotu.
Poznámka: Předpokládejte, že předané teplo je přímo úměrné rozdílu teplot tělesa a okolí, teplota tělesa se tedy bude exponenciálně přibližovat teplotě okolí.
4. válec versus kvádr
Mějme homogenní válec a homogenní kvádr. Obě tělesa jsou vyrobena ze stejného materiálu a mají stejnou hmotnost. Hodíme je současně vedle sebe na stůl stejnou počáteční rychlostí $v_{0}$ (hodíme je rovnoběžně s rovinou stolu, svislá složka rychlosti při dopadu je nulová). Válec se na počátku neotáčí. Rozhodněte, které těleso se bude pohybovat rychleji, případně diskutujte fáze pohybu, kdyby se jejich vzájemná pozice s časem měnila. Uvažujte pohled jak silový, tak energetický. Uvažujte, že smyková třecí síla je charakterizovaná pouze součinitelem smykového tření, tj. základní model, kdy smyková třecí síla závisí pouze na normálové přítlačné síle. Valivé tření neuvažujte.
P. záplavy ve vesmíru
Uvažujme vesmír se stejnými fyzikálními zákony, který je však vyplněn z větší části kapalnou vodou. Ve vodě se vyskytují drobné bublinky plynu, jejichž hustota je značně menší, než je hustota vody. Budou se tyto bublinky vzájemně přibližovat nebo vzdalovat?
E. fyzik hudebníkem
Změřte součinitel klidového tření mezi různými materiály (např. papír a dřevo). Při měření využijte gramofonu.
S. kvantovka
- V kvantové mechanice má smysl řešit i jednorozměrné úlohy, to znamená uvažovat částice, které se mohou pohybovat pouze ve směru osy $x$ a jejichž vlnová funkce $ψ(x)$ závisí pouze na $x$.
Podívejme se na nejjednodušší z nich, na částici v „nekonečně hluboké potenciálové jámě“. Tím máme na mysli částici, která se nemůže vyskytovat jinde, než v oblasti $x$ náleží $(0,L)$, takže její vlnová funkce je vně této „jámy“ o šířce $L$ nulová. Uvnitř potenciálové jámy se částice může pohybovat zcela volně, protože na ni nepůsobí žádné síly. Obrazně řečeno, uvnitř nekonečné potenciálové jámy má částice potenciální energii nulovou a vně nekonečnou. Vaším úkolem je napsat vlnové funkce odpovídající všem možným stavům systému, víte-li, že každá vlnová funkce této částice je v intervalu $[0,L]$ harmonická (tj. ve tvaru $c_{1}\sin(kx) + c_{2}\cos(kx)$, $c_{1}$, $c_{2}$ jsou komplexní čísla, $k$ je reálné) a na jeho krajích nulová. S pomocí faktu, že perioda této harmonické funkce je rovna de Broglieho vlnové délce, určete všechny možné energie, které částice může mít. Nakonec se ještě pokuste získané vlnové funkce nanormovat.
- Vypočítejte, s jakou pravděpodobností se elektron nachází v jádře iontu $\jd{He}^{+}$, když je ve stavu $1s$, kterému odpovídá normovaná vlnová funkce: $$ψ(\textbf{r}) = \sqrt{\frac{Z^{3}}{πa_{0}^{3}}}e^{(-Zr/a_{0})}\,,$$ kde $Z$ je protonové číslo helia a $a_{0}$ Bohrův poloměr atomu vodíku. Pokud tuto pravděpodobnost neumíte vypočítat přesně, pokuste se ji odhadnout seshora i zezdola, abychom znali alespoň její řád.
- Napište prostorovou závislost $ψ(\textbf{r}_{1},\textbf{r}_{2})$ vlnové funkce soustavy dvou elektronů v základním stavu atomu helia při zanedbání interakce mezi nimi.
Literatura: Arthur Beiser: Úvod do moderní fyziky, Academia, Praha 1978.