3. Série 19. Ročníku
Termín uploadu: -
1. dotyk koule a válce
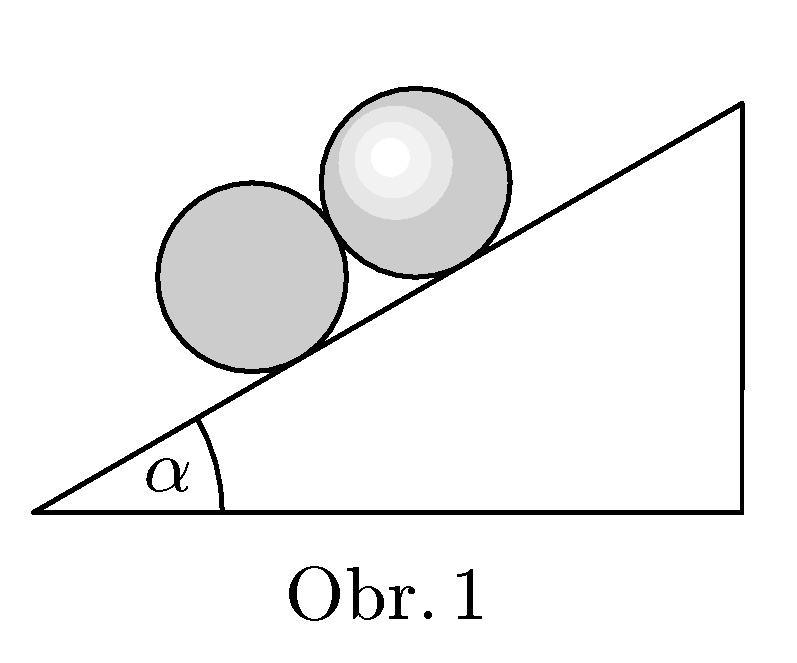
Koule a válec o stejném poloměru a stejné hmotnosti jsou vyrobené z různých materiálu a leží na nakloněné rovině tak, že se vzájemně dotýkají. Určete, za jakých podmínek zůstanou ležet v klidu.
Řešil Petr Sýkora při TJUFu.
2. nájezd na čočku
Mějme spojku o ohniskové vzdálenosti $f$. Zdroj světla je na ose ve vzdálenosti $a>f$ od čočky, za kterou vzniká jeho obraz. Zdrojem začneme pohybovat určitou rychlostí směrem k čočce. Určete, jak rychle se pohybuje obraz. Rozhodněte, zda tato rychlost může být i nadsvětelná. Bylo by to v rozporu s principy speciální teorie relativity?
Vymyslel Jarda Trnka, když psal studijní text z optiky.
3. odložená koupel
Robin se rozhodl, že se po půl roce vykoupe. Napustil si vanu teplou vodou o teplotě $T_{1}$ a objemu $V_{1}$. Ke koupání ale zase nedošlo. Napadlo ho, že je to zbytečné plýtvání energií, teplo z vany totiž lze použít i lépe.
Robin je šikovný a umí si vyrobit libovolný tepelný stroj, proto si už dávno chtěl izotermicky stlačit plyn o teplotě $T$, objemu $V_{0}$ a hustotě $ρ$. A tady k tomu dostal ideální příležitost. Jako chladič použil okolní vzduch, jehož množství je nevyčerpatelné a jehož teplota je $T_{2}$. Určete, na jaký minimální objem $V$ lze tento plyn stlačit, použije-li k tomu Robin teplou vodu ve vaně a svůj tepelný stroj.
4. stoupavý proud
Letadlo letí vodorovně rychlostí o velikosti $v$ a najednou vlétne do stoupavého proudu o rychlosti velikosti $v′$. Jaké bude počáteční vertikální zrychlení letadla těsně po nalétnutí do stoupavého proudu?
Předpokládejte, že součinitel vztlaku $C$ (koeficient v Newtonově vzorci pro vztlak) závisí lineárně na úhlu, který svírá směr proudění vzduchu s rovinou křídla.
Navrhl Matouš Ringel, když mu úlohu odmítl prof. Volf.
P. udýchaný běžec na ledě
Jedno pozdní zimní odpoledne se šel Matouš proběhnout na zamrzlý broumovský rybník. Matouš chvilku běžel, ale po pár metrech už nemohl a zastavil se. V zápětí se však pod ním led prolomil a Matouš zahučel pod vodu. Vysvětlete, proč se při běhu pod Matoušem led neprolomil a po zastavení ano?
Úloha ze sbírky Dr. Kapicy.
E. a jsou tu zase hody!
V Černvíře je veselo, všichni tancují, baví se, ale hlavně pijí alkoholické nápoje. Ne však každý se chce co nejdříve opít. Mezi místními stárky je jeden, kterému jde zejména o vědecký výzkum. Po vypití dvou litrů levného stolního vína ho napadlo, že by mohl zjistit, kolik toho alkoholu do sebe vlastně dostal. Nebyl ovšem v natolik střízlivém stavu, aby experiment zrealizoval. Zkuste to tedy vy!
Změřte, jaký je hmotnostní podíl alkoholu obsažený v levném stolním víně, a výsledek porovnejte s hodnotou na obalu.
Našel Jarda Trnka na internetu a vzpomněl si při tom na jednoho z organizátorů.
S. aplikace statistické fyziky
- Pomocí podobné úvahy jako v příkladu v textu určete, jaký tvar má Gultbergův-Waageův zákon pro složitější reakce (např. $2A+B -> A_{2}B$). Zkuste zjistit, jestli (a jak dobře) tento zákon odpovídá skutečnosti.
- Maxwellova-Boltzmannova rozdělení odvoďte, jaké mocnině teploty je úměrná střední kinetická energie částic plynu. Ověřte si, že jste schopni stejnou metodou zjistit, jak závisí na teplotě střední hodnota libovolné mocniny rychlosti.
- Mějme systém nezávislých spinů, diskutovaný v textu, o teplotě $T_{1}$, který se nachází v magnetickém poli o velikosti $B_{1}$. Následně systém adiabaticky zaizolujeme (tj. zavřeme jej do termosky, aby z něj nemohlo odcházet žádné teplo) a budeme pomalu zmenšovat magnetické pole až na hodnotu $B_{2}$. Kvalitativně vysvětlete, proč se bude snižovat teplota systému. Pokud možno vypočítejte, jaká bude výsledná teplota $T_{2}$.
Nápověda: Práce vykonaná na systému s magnetickým momentem $M$ při malé změně magnetického pole $B$ o $\rm{d}B$ je dána vztahem $\rm{d}W=-MdB$.
Autor seriálu, Matouš Ringel.