5. Série 21. Ročníku
Termín uploadu: -
1. pozor, neudus se
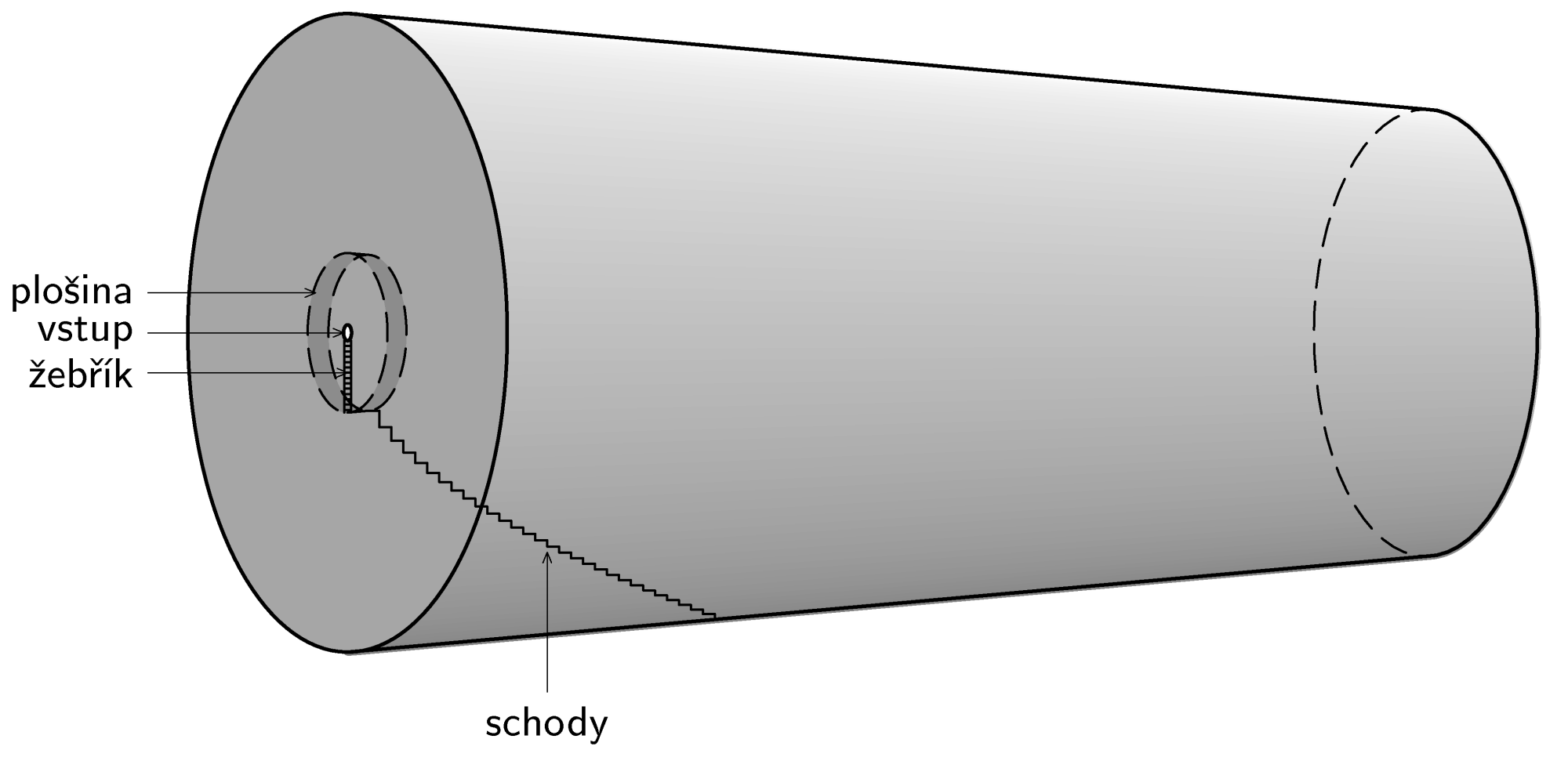
V páté sérii opustíme fyziku a vykročíme do světa sci-fi. Vesmír brázdí nemálo kosmických lodí a také Ráma (A. C. Clarke: Setkání s Rámou, Návrat Rámy, Zahrady Rámovy, Ráma tajemství zbavený). Ráma je obří mezihvězdné plavidlo zkonstruované mimozemskou civilizací, která připlula do sluneční soustavy. Připravíme vás na odvážnou výpravu do jeho nitra a zamyslíme se nad strastmi, které na vás číhají.
Ráma má tvar válce o délce $54\,\jd{ km}$ a vnitřním průměru $16\,\jd{ km}$. Jeho vnitřek je vyplněn vzduchem. Ráma má dokonce svou vlastní umělou gravitaci, která vzniká tím, že se otáčí kolem své osy jednou za čtyři minuty. Na vnitřním povrchu pláště má vzduch tlak jedné atmosféry.
Vstup do Rámy je otvor uprostřed jedné podstavy. Předtím, než vstoupíš a sundáš si skafandr, si však rozmysli, zda je na jeho ose dýchatelný vzduch. Jaká je jeho hustota v porovnání s hustotou na vnitřním povrchu, je-li teplota vzduchu všude stejná?
Martin Formánek a Kuba Benda
2. otázka přežití
Od vchodu vede k vnitřnímu povrchu žebřík. Již jsi po něm sestoupil kilometr, když vtom jsi neopatrně sklouzl a pustil se žebříku. Jakou rychlostí dopadneš na povrch Rámy a za jak dlouho? Máš šanci přežít?
Martin Formánek
3. schody z nebe
Žebřík vede jen dva kilometry na plošinu, ze které se dále sestupuje po schodech, jež se mohutným obloukem klenou nad krajinou. Schodiště má zvláštní tvar. Je totiž postavené tak, že se na každý krok vynaloží stejná práce. Odvoď, jak závisí výška schodu na vzdálenosti od osy Rámy, pokud je délka schodů konstantní. Také můžeš určit, jaký tvar má onen oblouk.
Martin Formánek
4. sluneční konzerva
Ráma cestuje mezi hvězdami tak, že polovinu času rovnoměrně zrychluje a polovinu času rovnoměrně zpomaluje. Právě se pohybuje kolem Slunce po parabole s vrcholem na orbitě Země. Energii získává ze slunečního záření (žádný reaktor nebo obří baterie jsi na něm neobjevil) a jeho povrch absorbuje 80 % dopadající energie. Nasbírá při průletu sluneční soustavou dostatečnou energii, aby se dostal k Siriu, který je vzdálen 12 světelných let, za 24 let?
Nadhodil Jakub Benda
P. rámatřesení
Úspěšně ses dostal na povrch Rámy. Z ničeho nic se Ráma několikrát otřásl a zdá se ti, že se změnila rychlost jeho rotace. Tato otázka tě velice tíží. Navrhni proto několik způsobů, jak bys změněnou periodu rotace určil.
Martin Formánek
E. životní etapy Ramy
Bude mít Rama jiné fyzikální vlastnosti, poté co ji roztavíte a opět necháte ztuhnout? Doporučujme měřit hustotu, viskozitu či barvu.
Vytlačil Marek Pechal.
S. posloupnosti, horká dutina a bílý trpaslík
- Odvoďte Taylorův rozvoj exponenciály a pro $x=1$ graficky znázorněte posloupnost částečných součtů řady $\sum_{k=1}^{∞}1⁄k!$ spolu s posloupností ${ ( 1 - 1 ⁄ n)^{n}}_{n=1,2,\ldots}$.
Stejným způsobem porovnejte posloupnost ${ ( 1 - 1 ⁄ n)^{n}}_{n=1,2,\ldots}$ a posloupnost částečných součtů řady $\sum_{k=1}^{∞}x^{k}⁄k!$, čili posloupnost ${\sum_{k=1}^{n}x^{k}⁄k!}_{n=1,2,\ldots}$, tentokráte však pro $x=-1$.
- Druhý úkol bude určit závislost koncentrace elektronů a pozitronů na teplotě při celkovém náboji $Q=0$ v prázdné uzavřené horké dutině.
(Bude-li se vám chtít, i při jiných vámi zvolených hodnotách $Q.)$ Dále určete závislost poměru vnitřní energie $U_{e}$ elektronů a pozitronů ku celkové vnitřní energii systému $U$ (tj. součtu energie elektromagnetického záření a částic) na teplotě a určit hodnoty teploty odpovídající některým význačným hodnotám tohoto poměru (např. 3 ⁄ 4, 1 ⁄ 2, 1 ⁄ 4, …; může tento poměr nabývat všech těchto hodnot?).
Pokuste se své výsledky pěkně graficky zpracovat ve formě grafů (můžete zkusit i trojrozměrné).
Při vašem snažení vám může hodně pomoci, pokud si zavedete vhodné bezrozměrné jednotky (např. $βE_{0}$ místo $β$ apod.).
- Řešte soustavu diferenciálních rovnic pro $M(r)$ a $ρ(r)$ v modelu bílého trpaslíka pro několik vhodně zvolených hodnot $ρ(0)$
a pro každou z nich sledujte hodnotu, ke které se blíží $M(r)$ při $r→∞$. Ta je zřejmě rovna hmotnosti celé hvězdy. Pokuste se prozkoumat závislost této celkové hmotnosti na $ρ(0)$ a odhadnout její horní mez. Srovnejte váš výsledek s horní mezí hmotnosti bílého trpaslíka, kterou najdete v literatuře nebo na internetu. Uvažujte, že je hvězda tvořena héliem.
Zadali autoři seriálu Marek Pechal a Lukáš Stříteský.