6. Série 25. Ročníku
Termín uploadu: -
(2 body)1. tref svojí družici
Máme malý míček o poloměru $r$ těsně nad míčem o poloměru $R$. Nejspodnější bod spodního míče je ve výšce $h$ nad zemí. Oba míčky pustíme. Do jaké nejvyšší výšky může vystoupit horní míček? Uvažujte, že všechny srážky jsou dokonale pružné. Bez újmy na bodech můžete považovat hmotnost horního míčku za zanedbatelnou.
Bonus: Postup zobecněte na $N$ míčků. (Stále můžete uvažovat, že hmotnost míčku výše je zanedbatelná oproti míčku pod ním.)
Potrefený Karel.
(2 body)2. kosmická stanice
Odhadněte, jakou minimální energii musíme dodat kosmické stanici, abychom ji dostali na oběžnou dráhu. Můžete pracovat s hodnotami pro mezinárodní kosmickou stanici ISS, která obíhá Zemi ve výšce cca $h=350\;\mathrm{km}$ a má celkovou hmotnost přibližně $m=450\;\mathrm{tun}$. Vysvětlete, proč je odhad minimální a vyjmenujte alespoň některé fyzikální skutečnosti, které vedou k tomu, že je skutečná spotřeba raket významně vyšší.
Astrokarel.
(4 body)3. čerpadlo
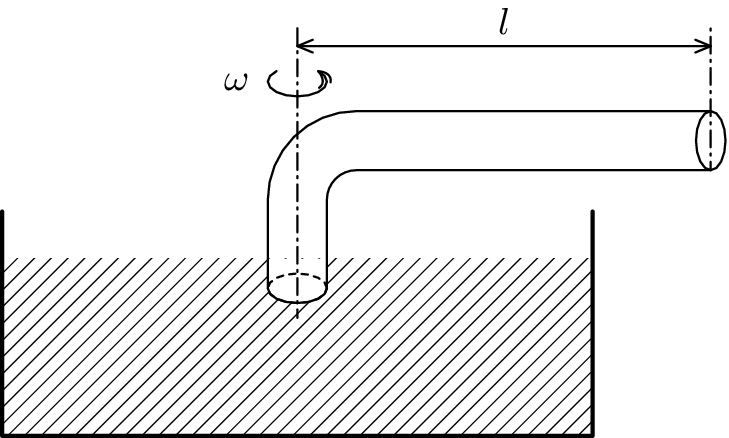
Mějme zahnutou trubici délky $l$ plnou vody, jejíž spodní konec je ponořen do nádoby. Trubicí otočíme jednou za čas $T$. Pod jakým tlakem je nasávána voda z nádobky? Viskozitu vody a tlak sloupce vody ve svislé části zanedbejte.
Vyčerpaný Petr.
(4 body)4. kroule
Jaká část povrchu ledové kry tvaru koule trčí nad hladinu? Hustota ledu je $917\;\mathrm{kg/m^3}$, hustota mořské vody $1025\;\mathrm{kg/m^3}$.
(4 body)5. běh na přednášku z eugeniky
Aleš sedí pod kopcem u stanu a surfuje na internetu na svém tabletu, když tu si náhle všimne, kolik je hodin a uvědomí si, že vlastně chtěl jít na přednášku. Už je tak pozdě, že bude muset celou cestu běžet a nebude moct zastavit, ani aby se vydýchal. Proto se samozřejmě okamžitě rozběhne svou maximální běžeckou rychlostí $v$ do kopce, který má rovnoměrné stoupání $α$. Po chvíli (čas $T)$ si ale uvědomí, že má v kapse cihlu a že tu cihlu chtěl nechat u stanu. Aleš od sebe umí cihlu hodit jedině rychlostí $w$. Pod jakým úhlem má cihlu v tom okamžiku vyhodit, aby dopadla na kamaráda, co si právě sedl na jeho místo? Může se stát, že nedohodí? Aleš je hodně rychlý, a proto neuvažujte jeho reakční dobu a ani dobu, kterou vám zabere řešení úlohy.
Karel civěl na internet.
(4 body)P. paprsky X
Při prosvěcování prstů silným světlem je možno vidět jednotlivé cévy, ale zbytek tkáně se zdá homogenní. Vysvětlete, proč cévy vidět jsou, zatímco kosti ne.
Michal a LEDky.
(7 bodů)E. plechová komprese
Skvělý způsob, jak rozdrtit prázdnou plechovku od coly (pokud se vám ji nechce drtit o svou hlavu a vlastně se vám nechce ji vůbec manuálně drtit), je kápnout na dno trochu vody, trochu utěsnit otvor v ní a dát ji na vařič zahřát. Když ji pak rychle ponoříte do studené vody, tak se vám s trochu šikovnosti krásně zdrtí. Vyzkoušejte si to a vyzkoušejte to i bez toho, že by v plechovce byla voda. Vysvětlete, proč to funguje jinak s vodou a bez ní, a zkuste svoji plechovku zdrtit na co nejmenší objem vůči původnímu. Ten změřte a popište podmínky, při kterých se vám to podařilo. Pošlete fotky zdrcených plechovek. Pozor Při dělání pokusu k úloze se nespalte!
Karel chtěl, aby se účastníci spálili stejně jako on.
(6 bodů)S. seriálová
- Vyjděte z Newtonova modelu vesmíru odvozeného v seriálu. Pro $E = 0$ vyřešte případ, že vesmír se rozpíná a hustota energie vakua se nemění. Odhadněte, jaká je na základě tohoto modelu budoucnost vesmíru.
- Pokud je vesmír plný hvězd, jistě k nám dřív nebo později dorazí světlo z každé hvězdy. Jak je možné, že je i přes to v noci tma? Zdůvodnění zkuste podpořit i kvantitativními odhady.
- V seriálu je uvedeno, jak odvodit existenci temné hmoty na kupě galaxií pomocí poměrně jednoduchého modelu. Zkuste navrhnout další způsob, jak dokázat existenci temné hmoty v kupách galaxií. Není třeba nutně podpořit výpočtem, stačí jednoduchý návrh.
Janapka.