5. Série 29. Ročníku
Termín uploadu: -
(2 body)1. už to teče
Tenký drát s odporem $R=100\;\mathrm{mΩ}$ a délkou $l=1\;\mathrm{m}$, který je připojen ke zdroji stejnosměrného napětí $U=3\;\mathrm{V}$, obsahuje ve svém objemu $N=10^{22}$ volných elektronů, kterými přispívá k toku elektrického proudu. Určete, jak velkou průměrnou (přesněji střední) rychlostí se elektrony v drátu pohybují.
Mirek už zase slyšel, že částice ve vodiči tečou rychlostí světla.
(2 body)2. mnohočásticová
Mějme nádobu, která je pomyslně rozdělena na dvě shodné disjunktní oblasti $\mathrm{A}$ a $\mathrm{B}$. V nádobě je $n$ částic, z nichž se každá nachází s pravděpodobností $50\; \%$ v části $\mathrm{A}$ a s pravděpodobností $50\; \%$ v části $\mathrm{B}$. Určete, s jakou pravděpodobností bude v části $\mathrm{A}$ $n_{\mathrm{A}}=0,\! 6 n$, resp. $n_{\mathrm{A}}=1+n/2$ částic. Řešte pro $n=10$ a $n=N_{\mathrm{A}}$, kde $N_{\mathrm{A}}≈6 \cdot 10^{23}$ je Avogadrova konstanta.
Mirek má rád zákon velkých čísel.
(3 body)3. egyptská brána
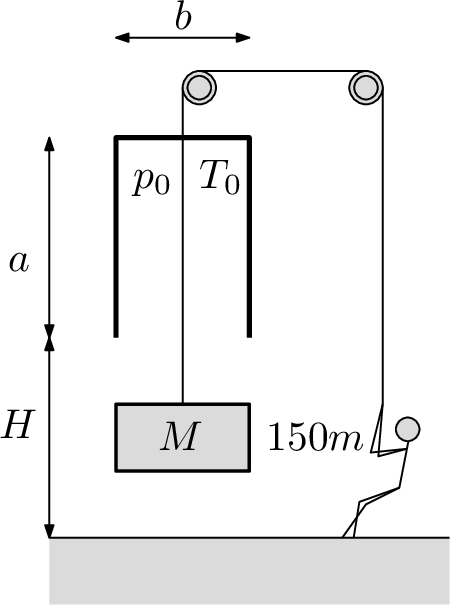
Ve starověkém Egyptu uměli vyrobit bránu, ale ještě neznali mříže, tak brány zavírali nilany (vápencovými kameny). Na obrázku vidíte $150$ otroků o hmotnosti $m=60\;\mathrm{kg}$, kteří právě velmi pomalu otevírají bránu zavřenou nilanem o hmotnosti $M=8\;\mathrm{t}$. Nilan přesně (vzduchotěsně) pasuje do konstrukce nad bránou ve tvaru kvádru, která má vnitřní rozměry $a=3\;\mathrm{m}$, $b=0,\! 5\;\mathrm{m}$ a $c=3\;\mathrm{m}$. Uvnitř konstrukce je na počátku tlak $p_{0}=100\; \mathrm{kPa}$ a teplota $T_{0}=300\; \mathrm{K}$ a je umístěna ve výšce $H=3\;\mathrm{m}$. Určete, jak vysoko jsou otroci schopni vlastní vahou nilan zdvihnout, jestliže se teplota vzduchu nemění.
Mirek rád předává otrockou práci jiným.
(4 body)4. bezpečná jízda
Máme auto, které se blíží kolmo ke zdi. Řidič, který v autě jede, by se ale chtěl přibližovat ke zdi bezpečně. Jaký by muselo mít auto průběh rychlosti, aby vzdálenost od auta ke zdi v každý okamžik odpovídala dráze, kterou by auto s okamžitou rychlostí v té chvíli urazilo za $T=2\;\mathrm{s}$?
Karel přemýšlel nad bezpečnou vzdáleností.
(5 bodů)5. Rolling Stones
Na nakloněné rovině stojí koule s nehomogenním rozložením hustoty. Známe úhel sklonu nakloněné roviny $α$, poloměr koule $R$ a vzdálenost $t$ těžiště koule od jejího středu. Pokud si označíme střed koule $S$, bod dotyku koule s rovinou $D$ a těžiště koule $T$, pak definujeme úhel $φ_{0}=∠DST$ jako úhel před začátkem pohybu. Těžiště se navíc nachází v rovině určené úsečkou $DS$ (normálou k rovině) a směrem z kopce dolů. V závislosti na těchto parametrech podrobně rozeberte, jak se bude dál vyvíjet pohybový stav koule. Koule na rovině neprokluzuje.
Tohle si chtěl Kuba spočítat už od mala.
(5 bodů)P. metrová
Jak všichni víme, v jeskyních střední Evropy je docela zima, okolo $4\; \dg\mathrm{C}$. Proč je v metru docela teplo celý rok? Uvolňuje se více tepla z přítomných lidí, nebo spíše z technického zázemí?
Napadla Lukáše při čekání na metro.
(7 bodů)E. fotografická
Pomocí digitálního fotoaparátu změřte frekvenci střídavého proudu v síti. Postačí i chytrý telefon s vhodnou aplikací, která umožní nastavit přesnou hodnotu expozičního času.
Populární přednášky z fyziky na střední.
(6 bodů)S. přirozeně proměnná
- Použijte vztah pro entropii ideálního plynu $S(U,V,N)$ z řešení třetí seriálové úlohy
$$S(U,V,N) = \frac{s}{2}n R \ln{\left( \frac{U V^{\kappa -1}}{\frac{s}{2}R n^{\kappa} } \right)} nR s_0$$
a vztah pro změnu entropie
$$\mathrm{d} S = \frac{1}{T}\mathrm{d} + U \frac{p}{T} \mathrm{d} V - \frac{\mu}{T} \mathrm{d} N$$
a vypočítejte chemický potenciál jako funkci $U$, $V$ a $N$. Upravte dále na funkci $T$, $p$ a $N$.
Pomůcka: Přečtěte si o derivacích a malých změnách v druhém díle seriálu. Nyní by už mělo být zřejmější, že koeficienty jako $1/T$ před $\mathrm{d}U$ spočítáte jako parciální derivaci $S(U,V,N)$ podle $U$. Nezapomeňte na užitečný vztah $\ln{(a/b)}=\ln{a}-\ln{b}$ a že $n=N/N_{A}$.
Bonus: Vyjádřete tímto způsobem i teplotu a tlak jako funkce $U$, $V$ a $N$. Eliminujte závislost tlaku na $U$, abyste dostali stavovou rovnici.
- Je chemický potenciál ideálního plynu kladný, nebo záporný ($s_{0}$ považujte za zanedbatelné)?
- Co se bude dít s plynem v pístu, pokud je plyn napojený na rezervoár s teplotou $T_{\mathrm{r}}?$ Píst se může volně pohybovat a z druhé strany na něj nic nepůsobí. Popište, co se bude dít, pokud dovolíme jen kvazistatické procesy. Kolik práce takto dokážeme extrahovat? Platí, že se takto minimalizuje volná energie?
Pomůcka: Na výpočet práce se vám může hodit vztah $$\int _{a}^{b} \frac{1}{x} \;\mathrm{d}x = \ln \frac{b}{a}.$$
- Entalpii jsme definovali jako $H=U+pV$, Gibbsovu energii jako $G=U-TS+pV$. Jaké jsou přirozené proměnné těchto potenciálů? Jaké termodynamické veličiny dostaneme derivacemi těchto potenciálů podle svých přirozených proměnných?
- Vypočítejte změnu grandkanonického potenciálu $\textrm{d}Ω$ z jeho definičního vztahu $Ω=F-μN$.
Janči se snažil představit si chemický potenciál.