1. Série 10. Ročníku
Termín uploadu: -
1. stojánek na víno

Firma Strýček Skrblík s. r. o. zaplavila domací i zahraniční trhy geniálním výrobkem – dřevěným stojánkem na víno, jehož podobu si můžete prohlédnout na obrázku. Bude tento stojánek funkční? Závisí stabilita systému stojánek–láhev vína na velikosti a tvaru láhve či na množství moku v láhvi obsaženém? A pokud ano, tak jak?
2. alchymistické zrcadlo
Mějme válcovou nádobu se rtutí. Roztočíme ji úhlovou rychlostí $Ω$ kolem rotační osy. Určete ohniskovou vzdálenost zrcadla, které tvoří povrch rtuti.
3. ponořit, či neponořit
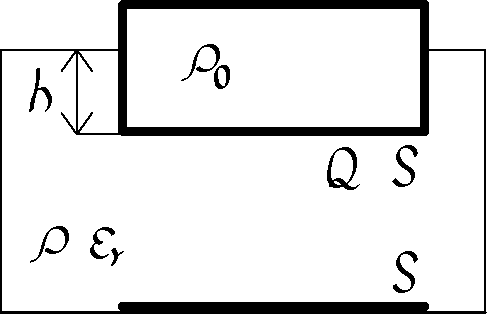
Velká nádoba je naplněna tekutým dielektrikem hustoty $ρ$ a relativní permitivity $ε_{r}$. Na dně nádoby je tenká kovová deska o ploše $S$. Nad ní plave vodivý hranol hustoty $ρ_{0}<ρ$, jehož podstava má obsah $S$. Na hranol přivedeme elektrický náboj $Q$ (viz obrázek). Jak ovlivní elektrické pole hloubku ponoru hranolu, víte-li, že
- deska na dně je uzemněna
- deska není uzemněna
Zaveďte takové zjednodušující předpoklady, abyste byli schopni úlohu řešit, a pokuste se odhadnout chybu, kterou vaše zjednodušení do výsledku vnesou.
4. překvapení po procitnutí
Představte si, že jdete večer klidně spát a do rána se veškeré vzdálenosti a rozměry všech přemetů zvetší desetkrát, přičemž jejich hmotnost se nezmění. Zanechá tato událost nějaké stopy na vaší existenci? A pokud ano, tak jaké?
P. balónek
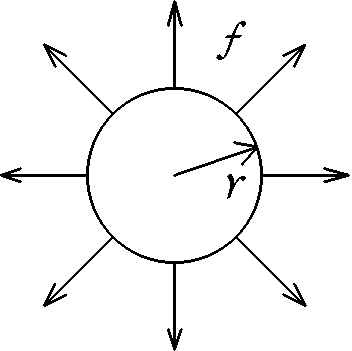
Jak moc můžete nafouknout pouťový balónek, dokud nepraskne? Předpokládejte, že balónek má tvar koule. Nenafouknutý nechť má poloměr $r_{0}$. Je z gumové blány, která má v přiblížení následující elastické vlastnosti.
Roztahujeme-li kruh vyříznutý z této blány na okraji tak, že síla na jednotku délky obvodu je $f$, bude poloměr kruhu $r$ přímo úměrný $f$, $r=r_{0}(1+af)$, $a$ je konstanta úměrnosti (viz obrázek). Materiál praskne při maximální síle na jednotku délky $f_{max}$. Na jedno nadechnutí naberete do plic objem $V_{fuk}$ vzduchu a ten pak fouknete do balónku. Kolikrát můžete do balónku fouknout, než praskne, a jaký bude mít rozměr?
E. výše mého domova hvězd se bude dotýkat
První experimentální úloha letošního ročníku je svým zadaní poměrně jednoduchá, poskytuje však velký prostor pro vaši nápaditost a vynalézavost: Změřte výšku vašeho bydliště co nejvíce způsoby a výsledky porovnejte. Nebojte se odvážných nápadů, originalita řešení bude kladně hodnocena. Spočítejte také nebo alespoň odhadněte chyby měření nezapomínajíce na to, že ve fyzice platí: jedno pozorovaní = žádné pozorovaní!
S. hvězdná velikost
Na procvičení pojmu hvězdné velikosti si vyřešte tyto úlohy:
- Jaká je absolutní magnituda Slunce $M$, je-li jeho zdánlivá magnituda $m=-26,74$?
- Složky dvojhvězdy Castor v souhvězdí Blíženců jsou v dalekohledu jasné $m_{A}=2,0$ a $m_{B}=2,9$. Neozbrojené lidské oko však tyto hvězdy nerozliší. Jak jasná se jeví tato dvojhvězda při pozorovaní pouhým okem?
- V jaké poloze na své dráze se jeví Venuše ze Země nejjasnější? Předpokládejte, že Venuše obíhá kolem Slunce přibližně po kružnici s poloměrem $r=0,7233\;\mathrm{AU}$ a že jasnost v celé viditelné a osvětlené části povrchu Venuše je konstantní. U těch, co neumějí derivovat, se spokojíme s numerickou hodnotou vzdálenosti Venuše od Země; nakreslete si graf závislosti jasnosti Venuše na vzdálenosti a odečtete z něj polohu největší jasnosti.
- Pokuste se odhadnout jasnost Venuše v poloze, kdy je na obloze od Slunce úhlově nejdál. Albedo Venuše (tj. poměr odražené ku dopadající intenzitě záření) je $0,76$ a její poloměr $R_{V}=6052\;\mathrm{km}$. Předpokládejte, že záření odražené od Venuše se rovnoměrně rozptýlí do celého poloprostoru a že jasnost každého světlého místa viditelného povrchu bude, jako by Slunce bylo právě nad ním.
- Určete, v jaké největší a nejmenší výšce nad obzorem se v naší zeměpisné šířce nachazí Slunce během roku. Rovina ekliptiky s rovinou zemského rovníku svírá úhel $23,5$ stupňů.