Vyhledávání úloh podle oboru

Jak rychle máme jít po visutém mostě, abychom jej co nejvíce rozkmitali? Úlohu vhodně parametrizujte a následně vyřešte.

Prodává se váleček, na kterém jsou malé výstupky. Váleček otáčeje se brnká o hranu ocelové destičky, která je nařezaná na proužky rozdílné délky. Ve skladbě na válečku se vyskytují všechny noty v daném neprázdném rozsahu (dejme tomu stupnice C dur). Dokážete zjistit tvar funkce konců nařezaných proužků?

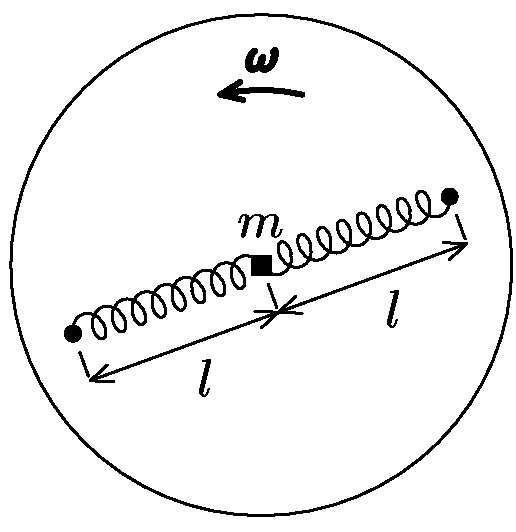
Kutil Mára si doma sestavil takovouto hračku: Na dřevěný kruh do jedné přímky procházející středem disku přimontoval dvě zarážky (stejně daleko od středu), mezi které na dvou pružinách o tuhosti $k$ napnul závaží o hmotnosti $m$. Závaží může bez tření klouzat po disku. Mára hračku položil na stůl a roztočil okolo osy disku úhlovou rychlostí $ω$, přičemž závaží mírně vychýlil z rovnovážné polohy. Kvalitativně popište pohyb závaží, a pokud si věříte, vypočítejte jej (za bonusové body).

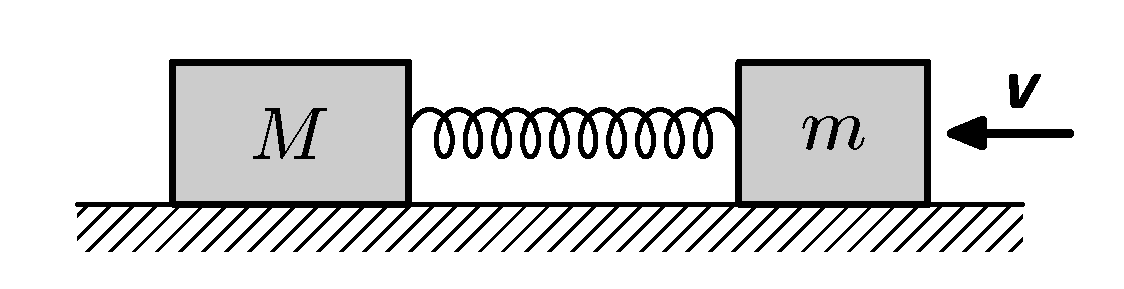
Dvě závaží o hmotnostech $m$ a $M$ jsou spojena pružinou o tuhosti $k$ a leží na hladké podložce (tření můžeme zanedbat). Tělesu $m$ udělíme rychlost $v$ (viz obrázek). Jaká bude nejkratší vzdálenost mezi tělesy a kdy jí dosáhnou?

Kačenka se rozhoupává na houpačce následujícím způsobem. Při největší výchylce houpačky se přikrčí, a když je houpačka v nejnižším bodě, opět se postaví. Tyto pohyby neustále opakuje. Poměr vzdálenosti těžiště Kačenky od osy otáčení při pokrčení a při stání je $2^{1⁄12} ≈ 1,06$. Kolikrát se Kačenka zhoupne, než se amplituda houpání zdvojnásobí?

Na zámořském parníku připravuje pro posádku jídlo kuchař Thomas. Na podávání talířů má šikovné zařízení. Pružinový držák udržuje vrchní talíř pořád ve stejné výšce. Vzdálenost mezi talíři je 1 cm. A protože je moře bouřlivé, sloupec 25 talířů pěkně kmitá. Jaká je frekvence těch kmitů?

Kroužením mokrým prstem po hraně broušené skleničky (například na víno) lze vyloudit poměrně intenzivní zvuk. Pokud se do skleničky nalije voda, pak frekvence vyluzovaného tónu klesá se vzrůstající výškou hladiny. Sami si to vyzkoušejte a pokuste se tento jev vysvětlit.

Kovová palička může kmitat okolo koncového bodu. Její druhý konec se stále dotýká kovového oblouku. Bod závěsu je přes kondenzátor kapacity $C$ zapojený na střed kovového oblouku (t.j. nejnižší bod, ve kterém se nachází dolní konec paličky). Celé kyvadélko se nachází v homogenním magnetickém poli indukce $B$, které je kolmé na rovinu kmitů. Jaká je doba kmitu kyvadla, pokud hmotnost paličky je $m$ a tření a odpor drátu zanedbáme. Počáteční výchylku kyvadla $\alpha_{0}$ uvažujeme menší než $5\, \jd{^{\circ}}$.

Spočtěte frekvenci malých radiálních kmitů gumového balónu. V balónu je $n$ molů plynu s Poissonovou konstantou $\kappa = 5/2$ o teplotě $T$. V případě, že rozdíl tlaků uvnitř a vně balónu, je nulový je poloměr balónu $r_{0}$. Plošná hustota gumy je v tomto případě $\rho_{0}$. Potenciální energie gumy je lineárně úměrná rozdílu jejího povrchu a povrchu klidového s konstantou úměrnosti $\sigma$. Tlak vně balónu je $p_{0}$. Hmotnost plynu je vůči hmotnosti balónu zanedbatelná.

Mějme rotační těleso o hmotnosti $m$. Na jeho ose zvolme body $A$ a $B$ vzdálené $d$. Zavěsíme-li těleso v bodě $A$, kývá se se stejnou periodou, jako když jej zavěsíme v bodě $B$. Moment setrvačnosti vzhledem k ose procházející těžištěm a kolmé na osu rotační symetrie je $J$. Určete všechny možné polohy těžiště tělesa vzhledem k bodům $AaB$.