Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (23)elektrické pole (71)elektrický proud (75)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (71)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (154)vlnění (51)
mechanika hmotného bodu
2. Série 10. Ročníku - S. oběžná dráha Země kolem Slunce
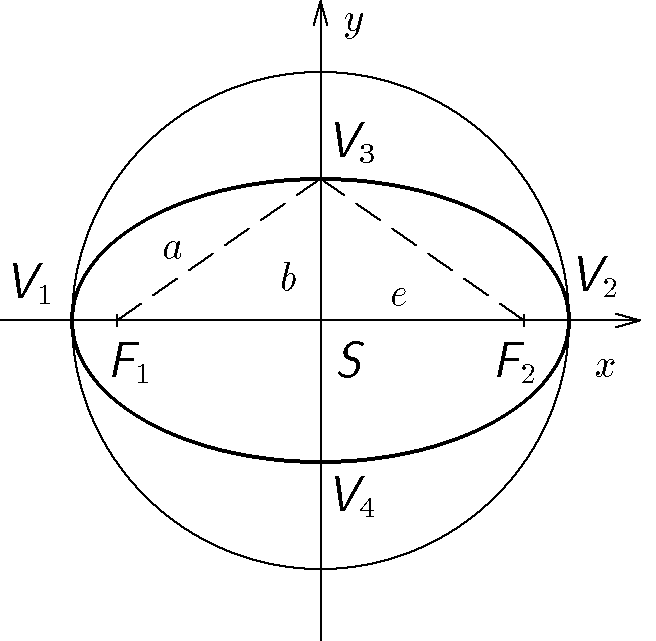
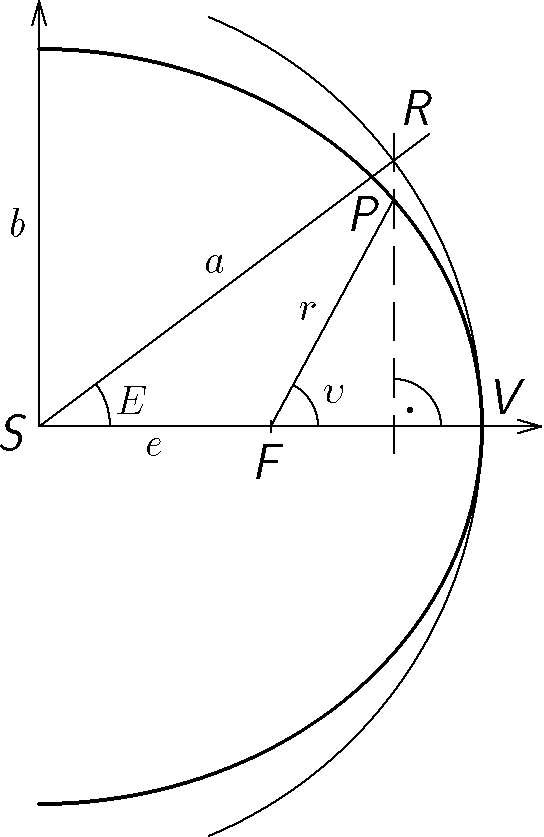
Určete pravou anomálii a vzdálenost Země od Slunce po $1/4$ oběžné doby Země kolem Slunce od průchodu Země periheliem. Velká poloosa je $a=1\;\mathrm{AU}$ a excentricita $e=0,0167$.
1. Série 10. Ročníku - 2. alchymistické zrcadlo
Mějme válcovou nádobu se rtutí. Roztočíme ji úhlovou rychlostí $Ω$ kolem rotační osy. Určete ohniskovou vzdálenost zrcadla, které tvoří povrch rtuti.
1. Série 10. Ročníku - 4. překvapení po procitnutí
Představte si, že jdete večer klidně spát a do rána se veškeré vzdálenosti a rozměry všech přemetů zvetší desetkrát, přičemž jejich hmotnost se nezmění. Zanechá tato událost nějaké stopy na vaší existenci? A pokud ano, tak jaké?
1. Série 10. Ročníku - E. výše mého domova hvězd se bude dotýkat
První experimentální úloha letošního ročníku je svým zadaní poměrně jednoduchá, poskytuje však velký prostor pro vaši nápaditost a vynalézavost: Změřte výšku vašeho bydliště co nejvíce způsoby a výsledky porovnejte. Nebojte se odvážných nápadů, originalita řešení bude kladně hodnocena. Spočítejte také nebo alespoň odhadněte chyby měření nezapomínajíce na to, že ve fyzice platí: jedno pozorovaní = žádné pozorovaní!
6. Série 9. Ročníku - 1. gejzír na betoně
Jednoho krásného dne se studentíci na jednom nejmenovaném gymnáziu nudili, a tak si vymysleli zábavu. Do igelitového pytlíku nabrali vodu a vyhodili jej z okna. Na betonovém chodníku to udělalo krásný gejzír. Ale co čert nechtěl – zrovna přišel do třídy profesor fyziky a zeptal se jich: „Z jaké výšky byste museli vyhodit ten pytlík z okna, aby vám ta voda přešla do varu?“ No, a my se vás ptáme na totéž. Můžete zanedbat odpor vzduchu, popřípadě zauvažovat, co by se stalo, kdyby tam odpor vzduchu byl.
6. Série 9. Ročníku - 4. žabák Břéťa
Na rybníce plave čtvercová deska o hmotnosti $M$ a straně $l$ a na jejím okraji sedí žabák Břéťa s tělesnou hmotností $m$. Jakou rychlostí a jakým směrem musí vyskočit, jestliže se chce trefit přesně na druhý konec desky? Předpokládejte, že se deska při odrazu minimálně ponoří, odpor prostředí můžete zanedbat.
5. Série 9. Ročníku - 1. řetízek babičky Julie
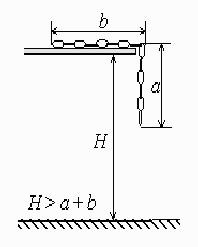
Na stole leží stříbrný řetízek po babičce Julii. Část, která je dlouhá $a$, visí přes hranu stolu, zbytek délky $b$ ještě leží na stole, jak je vidět na obrázku. Deska stolu je ve výšce $H$ nad podlahou, vše se nachází v klidu. V čase $t=0$ řetízek uvolníme a ten začne klouzat dolů ze stolu. Za jak dlouho spadne celý řetízek na zem (měřeno od chvíle, kdy se přestane dotýkat stolu)?
5. Série 9. Ročníku - 3. ucpaná roura
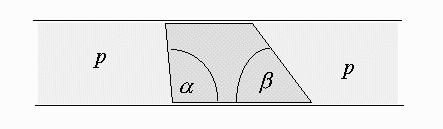
V trubce čtvercového průřezu $S$ (viz obrázek) je umístěn hranol se stěnami skloněnými o úhly $α$, $β$. Na obou stranách hranolu je plyn o tlaku $p$. Kterým směrem a s jakým zrychlením se začne hranol pohybovat, jestliže byl původně v klidu?
4. Série 9. Ročníku - 2. opilci v New Yorku
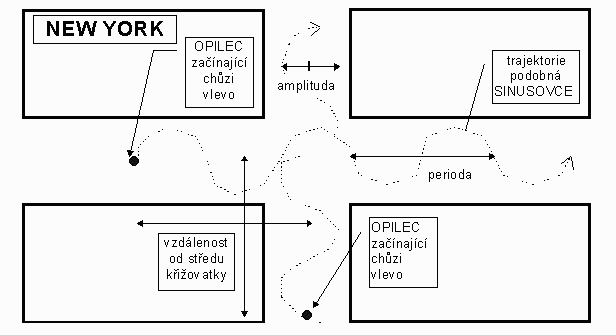
Dva kamarádi se po dlouhém nočním tahu ztratili kdesi ve spleti newyorských streets a avenues. Jak to odpovídá jejich stavu, procházejí ulice po křivce velmi blízké sinusovce s amplitudou $A=5\;\mathrm{m}$ a periodou $T=12{,}6\;\mathrm{m}$. Udržují konstantní rychlost potácení $v=1\;\textrm{m}\cdot \textrm{s}^{-1}$ (ve směru osy ulice). Shodou okolností se v jeden okamžik ocitnou oba ve vzdálenosti $l=27\;\mathrm{m}$ od téže křižovatky, každý však uprostřed jiné ulice (viz obrázek), přičemž oba směřují doleva od směru k průsečíku obou ulic. Určete, v jaké nejmenší vzájemné vzdálenosti se během průchodu křižovatkou ocitnou, předpokládáte-li, že oba směřují stále týmž směrem a jeden druhého si nevšímají.
Cílem této úlohy je, abyste se naučili pracovat se souřadnicemi, takže řešení nemusí být v obecném tvaru, můžete klidně zaokrouhlovat. Výsledky obdržené numericky budou posuzovány rovnocenně analytickému či grafickému řešení.
4. Série 9. Ročníku - 4. drama na schodech
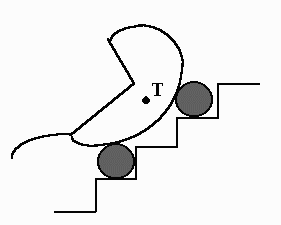
Starostlivá maminka se chystá se svým malým drobečkem na procházku do parku. Vytlačí kočárek ze dveří, zamkne je a teď už na ni čeká jen malá překážka – schody. Postupně zdolává první patro, druhé patro a stále se ne a ne objevit někdo, kdo by jí pomohl. Najednou si ale vzpomene, že nahoře zapomněla láhev se sunarem. Co kdyby se snad její mazlíček na procházce unavil a dostal hlad? Nechá tedy kočárek kočárkem a běží zpět nahoru. Odemkne dveře, jde do kuchyně, vezme láhev a vtom ji přeběhne mráz po zádech, vyrazí studený pot na čele, znovu ji přeběhne mráz po zádech a teprve potom si uvědomí proč. Vždyť nechala stát kočárek jen tak na schodech! (Řešitelé bez představivosti nechť si prohlédnou přiložený obrázek, kde $T$ značí těžiště.) Hrůzou nepříčetná běží záchranit, co se dá. Na vás zbývá dokončit tento příběh, co myslíte, kde nalezne kočárek se svým děťatkem?