Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (23)elektrické pole (71)elektrický proud (75)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (71)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (154)vlnění (51)
relativistická fyzika
1. Série 17. Ročníku - S. elektromagnetické pole
- V prostoru je homogenní magnetické a elektrické pole (homogenní pole má svou veličinu všude stejnou co do velikosti i směru). Je dána velikost
$E$ i $B$ a tyto vektory jsou na sebe kolmé. Jak se musí pohybovat elektron, aby na něj nepůsobila žádná síla? Jak je to v případě, že $E$ a $B$ svírají úhel $60^{\circ}$?
- Jak bylo řečeno v seriálu, nezmění se při přemístění jednoho z nábojů síla působící na druhý náboj hned. Pokuste se na základě tohoto faktu vysvětlit, proč má elektromagnetické pole hybnost.
Úlohy vymyslel autor seriálu Honza Houštěk.
5. Série 13. Ročníku - 4. letící tyč
Mějme v rovině dvě na sebe kolmé přímky $a$ a $b$. V přímce $a$ letí tyč délky $l=5\cdot 10^{7}\,\jd{m}$ rychlostí $v=6\cdot 10^{6}\;\mathrm{m}\cdot \mathrm{s}^{-1}$ (tyč je s přímkou rovnoběžná a její střed na ní neustále leží). Vaším úkolem je určit, jaký bude průběh „viděné“ (viz dále) délky tyče v závislosti na její vzdálenosti od průsečíku přímek. Tyč pozorujeme z přímky $b$ v takové vzdálenosti od průsečíku, která je zanedbatelná vůči vzdálenosti tyče od průsečíku.
„Viděná“ délka tyče: k přímce $a$ přiložíme pravítko a letící tyč vyfotografujeme. „Viděnou“ délkou tyče pak rozumíme rozdíl hodnot krajních bodů tyče odečtených z pravítka z fotografie.
2. Série 11. Ročníku - S. relace neurčitosti
- Před objevem neutronu existovala hypotéza, že jádro s atomovým číslem $Z$ a hmotnostním $A$ se skládá z $A$ protonů a $A-Z$ elektronů. Odhadněte řádově, jakou kinetickou energii by měl elektron, jehož neurčitost polohy by byla srovnatelná s velikostí jádra helia. Jaké důsledky má tento odhad pro zmíněnou hypotézu? Pokud se částice pohybuje rychlostí srovnatelnou s rychlostí světla, nelze již použít klasický vztah pro kinetickou energii $E_{k}=p^{2}⁄2\;\mathrm{m}$, a místo něj je třeba vzít relativistický vzorec:
$$E_{k}=\sqrt{(p^{2}c^{2}+m_{0}^{2}c^{4}} - m_{0}c^{2}\,,$$
kde $m_{0}$ je klidová hmotnost částice.
- Uvažujme výše popsaný dvojštěrbinový experiment s elektrony. Vzdálenost štěrbin je $b=0,3\;\mathrm{mm}$ a vzdálenost stínítka od přepážky $l=1\;\mathrm{m}$. Zjistěte, jakou rychlost musí mít elektrony, aby vzdálenost dvou sousedních interferenčních minim na stínítku, které může být sestaveno například z fotočlánků, byla $d=0,2\;\mathrm{mm}$.
- Představte si, že místo dvou štěrbin uděláme do přepážky pouze jednu. Po průchodu touto štěrbinou se fotony odchylují od původního směru, takže na stínítku uvidíme místo ostrého obrazu štěrbiny rozmazanou světlou skvrnu. Vysvětlete tento jev na základě relací neurčitosti.
Literatura: Arthur Beiser, Úvod do moderní fyziky, Academia, Praha 1978
2. Série 10. Ročníku - P. dvojčata ve vesmíru
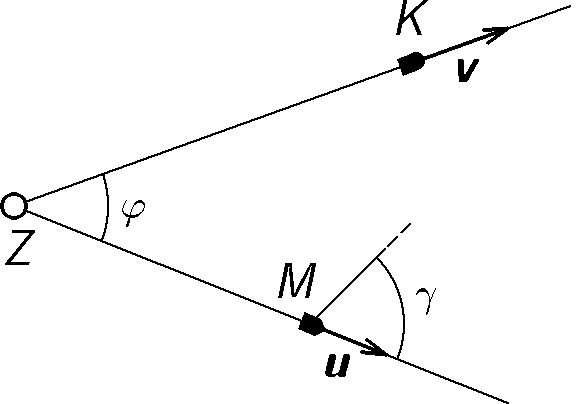
Michal a Karel jsou dvojčata. V zájmu vyššího vědeckého poznání je posadíme každého do jiné kosmické lodi v týž čas $t = 0$ a vystřelíme ze Země $Z$ rychlostmi $\textbf{u}$ a $\textbf{v}$ vstříc hvězdným dálavám. Abychom jim život co nejvíce znepříjemnili, jejich rychlosti svírají úhel $φ$, jak je to vidět na obr. 5. Po čas hvězdného putovaní se jejich rychlosti nemění. V čase $t_{0}$ se Michal, který se zrovna nachází v bodě $M$, rozhodne vyslat zprávu – radiový signál svému sourozenci. Pod jakým úhlem $γ$ vůči svému směru pohybu musí zaměřit signál, aby Karel zprávu obdržel?
Vliv ostatních těles na dráhu lodi a paprsku zanedbejte. Diskutujte též případ, kdy vesmírné lodě nejsou vypuštěny ve stejný čas, ale Michal se vydá do vesmíru o dobu $T$ dříve. Jak se změní výpočet budou-li velikosti rychlosti $\textbf{u}$ a $\textbf{v}$ blízké rychlosti světla $c$?
5. Série 7. Ročníku - S. prostoročas
- Nechť v bodě P dojde k jaderné explozi, při které vznikne mimo jiné množství nestabilních částic, jejichž maximální doba života je 10^{−6} s. Zakreslete do prostoročasového diagramu (jednou osou bude čas a druhou vzdálenost od bodu P) oblast světobodů, kde může dojít k registraci této částice. Jaká křivka ohraničuje tuto oblast?
- Tato úloha je zase více matematická. Ukázalo se, že délky pohybujících se tyčí jsou v diagramech zakresleny v jiném měřítku, než jaké odpovídá osám klidové soustavy (a v jakém jsme zvyklí měřit). Geometrie je zde tedy poněkud jiná než v běžné Eukleidovské rovině. Budeme v prostoročasové rovině považovat za pravý úhel mezi dvěma úsečkami rovnoběžnými s osami téže vztažné soustavy. Zkuste najít vztah pro převod úhlů mezi osami dvou různých vztažných soustav, tak jak je měříme běžným způsobem v klidové soustavě (kde určují rychlosti) a jak by to plynulo z goniometrických fcí pro poměr stran pravoúhlého trojúhleníka (podle uvedené definice pravého úhlu).
4. Série 7. Ročníku - S. zase paradoxy
- Po objasnění problému rytířů pro vás nebude obtížné vysvětlit následující paradox. Tyč délky $d$, která se pohybuje vysokou rychlostí (ve směru své délky) vodorovně těsně nad zemí, prolétá nad ústím kanálu, jehož klidová délka je taktéž $d$. V klidu by tyč do kanálu přesně zapadla, za pohybu se ale situace komplikuje. Z hlediska kanálu (klidová soustava) se tyč zkracuje, takže by měla hladce propadnout (tyč letí tak nízko, že nemůže kanál jednoduše přeletět a přitom jsou všechny její body stále ve stejné výšce), naopak pro tyč se zkrátil kanál a tedy nepřichází v úvahu, že by se do něj vešla. Jak to tedy dopadne?
- Opusťme již pozorování jen v jednom směru a podívejte se kolem sebe. Přeneste se do automobilu jedoucího značnou (tedy relativistickou) rychlostí dlouhou ulicí. Uvážíte-li relativistické efekty a konečnou rychlost šíření světla, jak se změní podoba ulice, okolních domů i silnice v dálce?
3. Série 7. Ročníku - S. současnost a paradox
- Pro události v oblastech 1 a 3, resp. 2 a 4 existuje vztažný systém, v němž jsou soumístné resp. současné události s událostí P. Časová, resp. prostorová souřadnice daných bodů v těchto systémech se pak nazývá vlastní čas, resp. vlastní vzdálenost. Určete, kolik činí tento čas, resp. vzdálenost pro bod o klidových souřadnicích $x$ a $ct$. Mají nějaké význačné postavení vzhledem k hodnotám v jiných soustavách souřadnic?
- Jedním z populárních paradoxů je příběh o dvou rytířích, kteří řeší svůj spor tak, že s absolutně tuhými dřevci stejné klidové délky vyjedou přímo proti sobě. Podle pohledu každého z nich je soupeřovo kopí relativisticky zkráceno a má tedy nad ním výhodu prvního úderu. Ovšem zjevně vítězství jednoho z nich nezávisí na vztažném systému. Rozřešte problém zakreslením situace v prostoročasovém diagramu s vyznačením poloh hrotů kopí a těl rytířů v klíčových okamžicích (klidovou soustavu volte spojenou jak se zemí, tak s jedním s rytířů).
2. Série 7. Ročníku - S. transformujeme
- Zjistěte, jaký výraz složený ze souřadnic $x$ a $t$ daného bodu se při změně vztažného systému nemění (je invariantní vúči Lorentzově transformaci).
- Víme, jak se ve vztažném systému dle diagramu určuje rychlost daného bodu. Pohybuje-li se vůči jedné soustavě daný bod rychlostí $u$, jakou rychlostí se pohybuje vzhledem k jiné soustavě, jejíž rychlost vůči první jest $v?$ Pokuste se odvodit spíše pomocí geometrických vztahů v diagramech než podle Lorentzových transformací.
1. Série 7. Ročníku - S. relativita
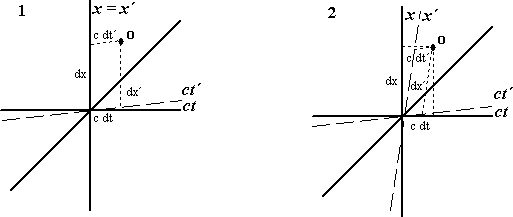
- Navrhněte postup (správný dle postulátů i a ii) synchronizace hodin.
- Všechny inerciální vztažné systémy jsou rovnocenné.
- Rychlost světla je ve všech soustavách stejná.
- Určete převod mezi souřadnicemi bodu O na diagramech 1 a 2, tj vztahy mezi d$x$ a d$x'$, resp. d$t$ a d$t'$, při dané rychlosti v (úseky d$x'$ a d$t'$ jsou rovnoběžné s osami $x'$ a $t'$, tlustá čára odpovídá rychlosti světla $c)$.
5. Série 2. Ročníku - 2. dvě fotografie
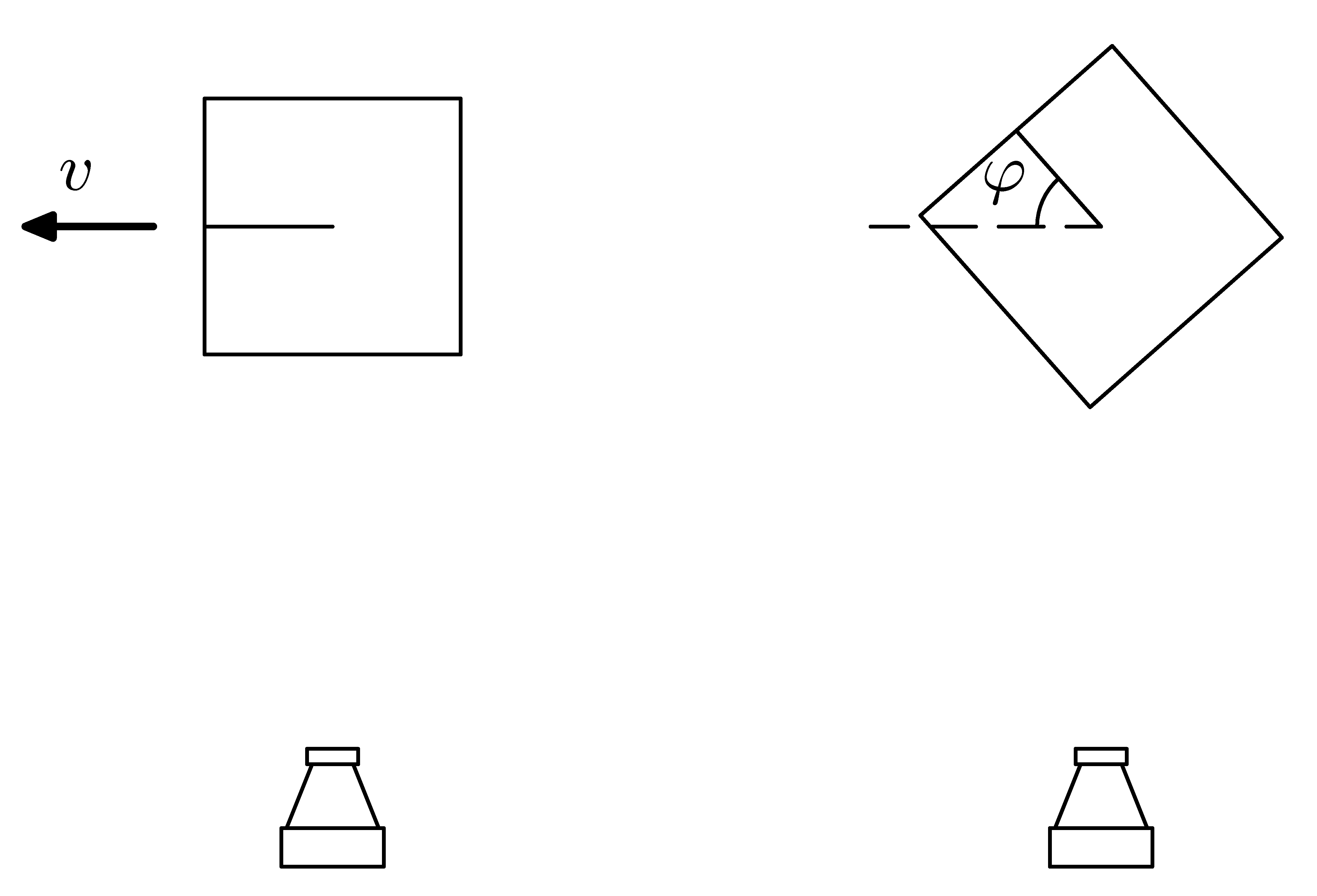
Fotky rakety
Fotograf v některém přístím století vyfotografoval raketu (pro jednoduchost tvaru krychle), a to jednou letící rychlostí blízkou rychlosti světla a jednou stojící, ale natočenou o úhel $φ=48,5°$ (obrázek). S údivem zjistil, že obě černobílé fotografie jsou totožné. Pomozte mu vysvětlit tento jev a spočtěte rychlost letící rakety.