Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (23)elektrické pole (70)elektrický proud (75)gravitační pole (80)hydromechanika (146)jaderná fyzika (44)kmitání (56)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (295)mechanika plynů (87)mechanika tuhého tělesa (220)molekulová fyzika (71)geometrická optika (77)vlnová optika (65)ostatní (165)relativistická fyzika (37)statistická fyzika (21)termodynamika (153)vlnění (51)
jaderná fyzika
6. Série 24. Ročníku - S. všehochuť
- Předpokládejme, že máme radioaktivní látku $X$, která se rozpadá na látku $Y$ s poločasem rozpadu $T_{1}$, ta se následně rozpadá na stabilní látku $Z$ s poločasem rozpadu $T_{2}$. Jak závisí koncentrace látky $Y$ na čase, pokud jsme na počátku měli pouze látku $X?$
- Vypočtěte, jak vypadá difrakční obrazec vzniklý průchodem světla o vlnové délce λ štěrbinou šířky $d$.
- Pokuste se najít frekvence ω, pro které existuje řešení vlnové rovnice na čtverci o hraně $a$. Kolik různých funkcí odpovídá jedné úhlové frekvenci?
Nápověda: Pro prostorovou část předpokládejte řešení ve tvaru $A(x,y) = X(x) Y(y)$.
Ozářilo Lukáše
5. Série 24. Ročníku - 4. zelená revoluce
Jaderná energie je stále kontroverzní zdroj energie a mnohé státy mají v úmyslu upouštět od jejich používání. Zaměřme se ale nyní na problém skladování jaderného odpadu. Představme si, že v roce 2000 bylo založeno zbrusu nové úložiště radioaktivního odpadu a navezen první čerstvý radioaktivní materiál, ale záhy bylo odsouhlaseno, že na úložiště bude každý další rok dovezeno o 5 % méně čerstvého radioaktivního odpadu než rok předchozí. Pro jednoduchost předpokládejme, že radioaktivní odpad má poločas rozpadu 100 let (běžný radioaktivní odpad má daleko delší poločas rozpadu). Poraďte obyvatelům přilehlých obcí, kterého roku se mohou těšit na nejvyšší dávku radiace, a umožněte jim tak třeba naplánovat založení rodiny. Při řešení můžete s výhodou použít váš oblíbený tabulkový procesor, třeba Excel nebo Calc.
Márovi se zalíbilo v Prypjati
6. Série 23. Ročníku - 3. atomový kondenzátor
Lukáš si koupil uranový atom a nenapadlo jej nic lepšího, než z něj postupně odebírat elektrony. Když odebral $n$-tý, s údivem zjistil, že se hmotnost atomu zvětšila. Co způsobilo tento jev? Jaké bylo ono $n?$
s pinzetou si hrál Lukáš L.
6. Série 23. Ročníku - 4. podkritické polokoule
Když Lukáše přestala bavit ionizace jednotlivých atomů, objednal si uranu víc. Doručili mu dvě přesné polokoule, každou o hmotnosti $m$ (splňující $m_{k}⁄2\lt m\lt m_{k}$, kde $m_{k}$ je kritická hmotnost). Lukáš je nastavil rovnými stranami k sobě a začal je přibližovat. V jaké vzdálenosti $d$ mezi koulemi byl jeho pokus přerušen zažehnutím řetězové reakce?
přinesl Pavel Motloch
5. Série 21. Ročníku - S. posloupnosti, horká dutina a bílý trpaslík
- Odvoďte Taylorův rozvoj exponenciály a pro $x=1$ graficky znázorněte posloupnost částečných součtů řady $\sum_{k=1}^{∞}1⁄k!$ spolu s posloupností ${ ( 1 - 1 ⁄ n)^{n}}_{n=1,2,\ldots}$.
Stejným způsobem porovnejte posloupnost ${ ( 1 - 1 ⁄ n)^{n}}_{n=1,2,\ldots}$ a posloupnost částečných součtů řady $\sum_{k=1}^{∞}x^{k}⁄k!$, čili posloupnost ${\sum_{k=1}^{n}x^{k}⁄k!}_{n=1,2,\ldots}$, tentokráte však pro $x=-1$.
- Druhý úkol bude určit závislost koncentrace elektronů a pozitronů na teplotě při celkovém náboji $Q=0$ v prázdné uzavřené horké dutině.
(Bude-li se vám chtít, i při jiných vámi zvolených hodnotách $Q.)$ Dále určete závislost poměru vnitřní energie $U_{e}$ elektronů a pozitronů ku celkové vnitřní energii systému $U$ (tj. součtu energie elektromagnetického záření a částic) na teplotě a určit hodnoty teploty odpovídající některým význačným hodnotám tohoto poměru (např. 3 ⁄ 4, 1 ⁄ 2, 1 ⁄ 4, …; může tento poměr nabývat všech těchto hodnot?).
Pokuste se své výsledky pěkně graficky zpracovat ve formě grafů (můžete zkusit i trojrozměrné).
Při vašem snažení vám může hodně pomoci, pokud si zavedete vhodné bezrozměrné jednotky (např. $βE_{0}$ místo $β$ apod.).
- Řešte soustavu diferenciálních rovnic pro $M(r)$ a $ρ(r)$ v modelu bílého trpaslíka pro několik vhodně zvolených hodnot $ρ(0)$
a pro každou z nich sledujte hodnotu, ke které se blíží $M(r)$ při $r→∞$. Ta je zřejmě rovna hmotnosti celé hvězdy. Pokuste se prozkoumat závislost této celkové hmotnosti na $ρ(0)$ a odhadnout její horní mez. Srovnejte váš výsledek s horní mezí hmotnosti bílého trpaslíka, kterou najdete v literatuře nebo na internetu. Uvažujte, že je hvězda tvořena héliem.
Zadali autoři seriálu Marek Pechal a Lukáš Stříteský.
4. Série 21. Ročníku - S. kvantový harmonický oscilátor
Modelujte časový vývoj vlnové funkce částice, kterou umístíme do potenciálu $V(x)=\frac{1}{2}kx$ a která je v čase $τ=0$ popsána vlnovou funkcí
$ψ_{R}(X,0)=\exp(-((X-X_{0}))⁄4)$,
ψ$_{I}(X,0)=0$.
Jedná se tedy o vlnový balík se středem mimo počátek. Prozradíme vám, že jde o tzv. koherentní stav harmonického oscilátoru a vlnový balík by měl harmonicky kmitat kolem počátku s úhlovou frekvencí $\sqrt{k⁄m}$ stejně jako klasická částice.
Pokud se vám toto podaří namodelovat, můžete vyzkoušet, jak se budou chovat vlnové balíky o jiné šířce (tedy se jmenovatelem v exponenciále odlišným od čtyř), případně jak bude situace vypadat při jiném průběhu potenciálu.
Zadal autor seriálu Marek Pechal.
2. Série 21. Ročníku - S. porcování divokých rovin
Skladování uranu
Palčivá otázka jaderné energetiky je skladování vyhořelého radioaktivního paliva. Většinou se skladuje ve válcových článcích ponořených ve vodní lázni, která drží jejich povrch na konstantní teplotě asi $20\,\jd{ °C}$. Na vás je nyní zjistit, jaké bude rozložení teploty v článcích tvaru kvádru se čtvercovou podstavou o hraně délky $20\,\jd{ cm}$. Článek bude poměrně vysoký a proto nás zajímá rozložení tepla v příčném řezu. Uran bude zaujímat koncentrický kvádr se čtvercovou podstavou o hraně $5\,\jd{ cm}$. Ze zkušenosti s válcovými kapslemi víme, že bude mít konstantní teplotu okolo $200\,\jd{ °C}$.
Zahřívající se drát
Máme velmi dlouhý drát kruhového průřezu o poloměru $r$ z materiálu o tepelné vodivosti $λ$ a měrné elektrické vodivosti $σ$. Přiložíme na něj konstantní elektrické napětí. Nechť je intenzita elektrického pole (tj. napěťový spád) uvnitř drátu konstantní, rovnoběžná s jeho osou a její velikost budiž $E$. Pak drátem bude procházet proud o plošné hustotě $j=σE$ a bude se vytvářet Jouleovské teplo s objemovým výkonem $p=σE$.
Protože materiál drátu má nenulovou tepelnou vodivost, vytvoří se v něm jisté rovnovážné rozložení teploty, které – jak víme – splňuje Poissonovu rovnici $λΔT=-p$. Předpokládáme, že okraj drátu udržujeme na dané teplotě $T_{0}$. Tím máme dánu okrajovou podmínku potřebnou k vyřešení rovnice. Vzhledem k symetrii problému se můžeme omezit na její řešení pouze ve dvou rozměrech – na průřezu vodiče (teplota jistě nebude záviset na posunutí podél osy vodiče). Nyní by již bylo jednoduché problém vyřešit popsanými metodami.
My si však situaci maličko zkomplikujeme a budeme předpokládat (zcela oprávněně), že měrná elektrická vodivost $σ$ závisí na teplotě. Budeme tedy mít rovnici typu $ΔT=f(T)$.
Pokuste se tuto rovnici numericky vyřešit pro nějakou danou závislost vodivosti na teplotě (můžete si ji najít v literatuře, na internetu, nebo si klidně nějakou vymyslet) a najít tak rozložení teploty na průřezu drátu. Můžete se pokusit měnit intenzitu elektrického pole $E$ a nakreslit voltampérovou charakteristiku drátu, vyzkoušet více druhů závislostí $σ(T)$ (třeba pro polovodič, jehož vodivost s rostoucí teplotou na rozdíl od obyčejného kovu roste) atd.
Vaší iniciativě samozřejmě meze neklademe a těšíme na pěkné nápady.
Kapacita krychle
Vypočítejte kapacitu dokonale vodivé krychle o straně délky $2a$. Pokud se budete nudit, můžete zkusit kvádr (a třeba závislost kapacity na délkách jednotlivých stran), případně jiné geometrické objekty.
Nápověda: Kapacita je poměr náboje na krychli rozmístěného ku potenciálu povrchu krychle (za předpokladu, že potenciál v nekonečnu je nulový). Problém tedy lze řešit tak, že si zvolíme libovolně potenciál krychle, vyřešíme Laplaceovu rovnici $Δφ=0$ vně krychle a vypočítáme celkový náboj na krychli užitím Gaussova zákona (tj. určením intenzity elektrického pole derivováním potenciálu a výpočtem jeho toku vhodně zvolenou plochou obklopující krychli).
Úplným řešením je vymyšlení vhodného fyzikálního modelu, návrh jeho numerického řešení a realizace této úlohy na počítači. Bodově ohodnotíme, pokud úlohu fyzikálně rozvážíte a okomentujete. Nějaký bod by se našel i za návrh algoritmu, který byste rádi počítači předložili.
Zadali autoři seriálu Lukáš Stříteský a Marek Pechal.
4. Série 20. Ročníku - 3. dostavba Temelína
Odhadněte tloušťku vody potřebnou k odstínění záření z jaderného reaktoru s výkonem $980\, \jd{MW}$ v plánovaném novém bloku JE Temelín. Z celkové energie uvolněné při štěpení jádra uranu připadne zhruba 82 % na kinetickou energii fragmentů, 6 % odnesou neutrina, po 6 % mají neutrony a gama fotony.
Nápověda: Pravděpodobnost, že částice projde materiálem do hloubky $d$, je přibližně rovna $e^{-σnd}$, kde $n=N/V$ je hustota molekul materiálu (v našem případě počet molekul vody v $1\, \jd{m^{-3}}$) a $σ$ je účinný průřez (cross section) pro absorpci částice na molekule. Účinný průřez má rozměr plochy ($\jd{m^2}$, často se užívá jednotka $\jd{barn} = 100\, \jd{fm^2}$) a závisí na energii částic. Hodnoty účinných průřezů se pokuste najít na internetu nebo v příslušných tabulkách.
Úloha řešil Karel Tůma na zkoušce z jaderné fyziky.
5. Série 19. Ročníku - 4. přírodní reaktor
Ve vzorku přirozeného uranu je 0,72 % izotopu $^{235}U$ s poločasem rozpadu 704 miliónů let a zbytek izotopu $^{238}U$, který má poločas rozpadu 4 468 miliónů let.
V sedmdesátých letech minulého století byla při těžbě uranu v oblasti Okla v rovníkovém Gabonu objevena ruda s relativním
zastoupením
izotopu $^{235}U$ 0,44 % . Tento nesoulad lze vysvětlit tím, že se v ložisku kdysi samovolně zažehl přírodní jaderný reaktor.
Určete, po jakou dobu jaderná reakce probíhala, bylo-li štěpení $^{235}U$ vyvoláno pomalými neutrony. Ke srážce nějakého pomalého neutronu s daným jádrem dojde průměrně jednou za 352 tisíc let.
Úloha ze zápočtové písemky z jaderné fyziky.
6. Série 18. Ročníku - 3. sonda NASA
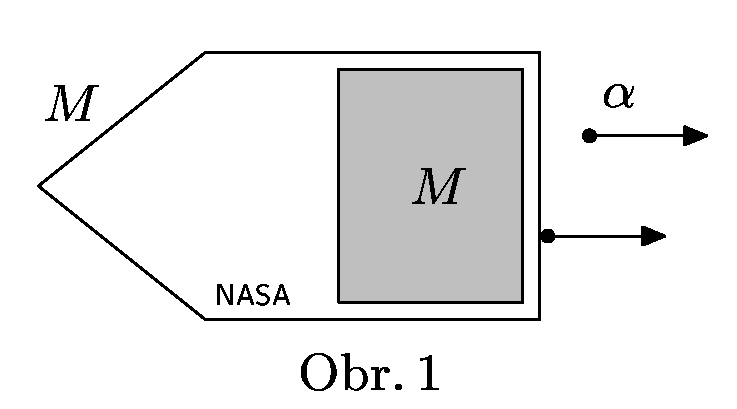
Jet Propulsion Laboratory v Kalifornii vyvíjí pro NASA nový typ raketových pohonů. Pohonná jednotka využívá hybnost $α$-částic při rozpadu nuklidu fermia $^{257}_{100}Fm_{157}$, jehož hmotnost je $m_{Fm}$ a poločas rozpadu $T$. Druhým produktem přeměny je nuklid kalifornia $^{253}_{98}{Cf}_{155}$. Hmotnost $α$-částice je $m_{α}$, hmotnost nuklidu kalifornia je $m_{Cf}$, přeměnou se uvolní energie $E$. Předpokládejte, že každá $α$-částice opouští raketu ve stejném směru.
Vesmírná sonda s popsaným pohonem je na počátku v klidu, její hmotnost je $M$, hmotnost pohonné látky je také $M$. Určete rychlost sondy $v$ po přeměně poloviny hmotnosti nuklidů fermia. Výslednou hodnotu dopočítejte i číselně pro hodnoty $E = 1,106\cdot 10^{-12}\, \jd{J}$, $M = 4\, \jd{kg}$ a $T = 100,5\, \jd{dní}$, ostatní hodnoty najdete v tabulkách.
SR olympiáda.